2022-03-13 更新: 添加 expert choice routing

2022-06-10 更新: Greg 和我撰写了这篇文章的缩短和升级版本，发表在 OpenAI Blog 上：“训练大型神经网络的技术”

近年来，我们在许多 NLP 基准任务上看到，更大的预训练语言模型能够取得更好的结果。但是，训练大型和深层神经网络具有挑战性，因为它需要大量的 GPU 内存和长时间的训练周期。

然而，单个 GPU 工作器的内存是有限的，许多大型模型的大小已经超过了单个 GPU 的容量。有几种并行计算范式可以实现跨多个 GPU 的模型训练，还有各种模型架构和内存节省设计，以帮助训练非常大的神经网络成为可能。

训练并行性

训练非常大的神经网络模型的主要瓶颈是对大量 GPU 内存的强烈需求，远远超过单个 GPU 机器所能承载的。除了模型权重（例如，数百亿的浮点数）之外，通常存储中间计算输出（如梯度和优化器状态（例如，Adam 中的动量和变异））的成本更高。此外，训练大型模型通常需要配备大型训练语料库，因此单个过程可能需要很长时间。

因此，必须采用并行计算。并行计算可以在不同维度进行，包括数据、模型架构和张量运算。

数据并行

最简单的 数据并行（DP） 方法是将相同的模型权重复制到多个工作节点，并将一部分数据分配给每个工作节点，以便同时处理。

如果模型大小大于单个 GPU 节点的内存，那么简单的 DP 就无法很好地工作。例如 GeePS 方法（Cui 等人，2016 ）将暂时未用的参数卸载回 CPU，以便在模型太大以至于无法装入一台机器时，仍能在有限的 GPU 内存下工作。数据交换传输应在后端进行，以免干扰训练计算。

在每个小批量（minibatch）结束时，工作节点需要同步梯度或权重，以避免陈旧。有两种主要的同步方法，每种都有明显的优缺点。

批量同步并行（BSP）：工作节点在每个小批量结束时同步数据。它可以防止模型权重的陈旧，并保持良好的学习效率，但每台机器都必须暂停并等待其他机器发送梯度。
异步并行（ASP）：每个 GPU 工作节点异步处理数据，无需等待或停滞。然而，它可能会导致使用陈旧的权重，从而降低统计学习效率。即使它增加了计算时间，也可能无法加速训练时间收敛。

中间的某个位置是在每隔 $x$ 次迭代（$x > 1$）时全局同步梯度。从 Pytorch v1.5 开始，这个功能在分布式数据并行（DDP ）中被称为“梯度累积”（Li 等人，2021 ）。桶化梯度避免了立即进行 AllReduce 操作，而是将多个梯度合并成一个 AllReduce 以提高吞吐量。可以根据计算图对计算和通信调度进行优化。

图 1. Pytorch DDP 的伪代码（图片来源：Li 等人，2021 ）

模型并行

**模型并行（MP）**旨在解决模型权重无法装入单个节点的情况。计算和模型参数被分布在多台机器上。这与数据并行不同，数据并行中每个工作节点都有整个模型的完整副本，而 MP 只在一个工作节点上分配一部分模型参数，因此内存使用和计算都得到了减少。

由于深度神经网络通常包含一堆垂直层，因此将大型模型按层分割，将一小组连续层组合成一个分区在一个工作节点上，看似很直接。然而，天真的实现通过多个这样的工作节点运行每个数据批次，而具有顺序依赖性，会导致大量等待时间的空泡，并严重低效利用计算资源。

图 2. 一个天真的模型并行设置，其中模型垂直分为 4 个分区。由于顺序依赖性，数据由一个工作节点一次处理，导致大量的空闲时间“泡泡”。(图片来源：Huang et al. 2019 )

管道并行

**管道并行（PP）**将模型并行与数据并行结合，以减少效率低下的时间“泡泡”。主要思想是将一个小批量分割成多个微批次，并使每个阶段的工作节点能同时处理一个微批次。注意，每个微批次需要两个传递，一个前向和一个后向。工作节点之间的通信只传输激活值（前向）和梯度（后向）。这些传递如何被调度，以及梯度如何被聚合，在不同的方法中有所不同。分区（工作节点）的数量也被称为管道深度。

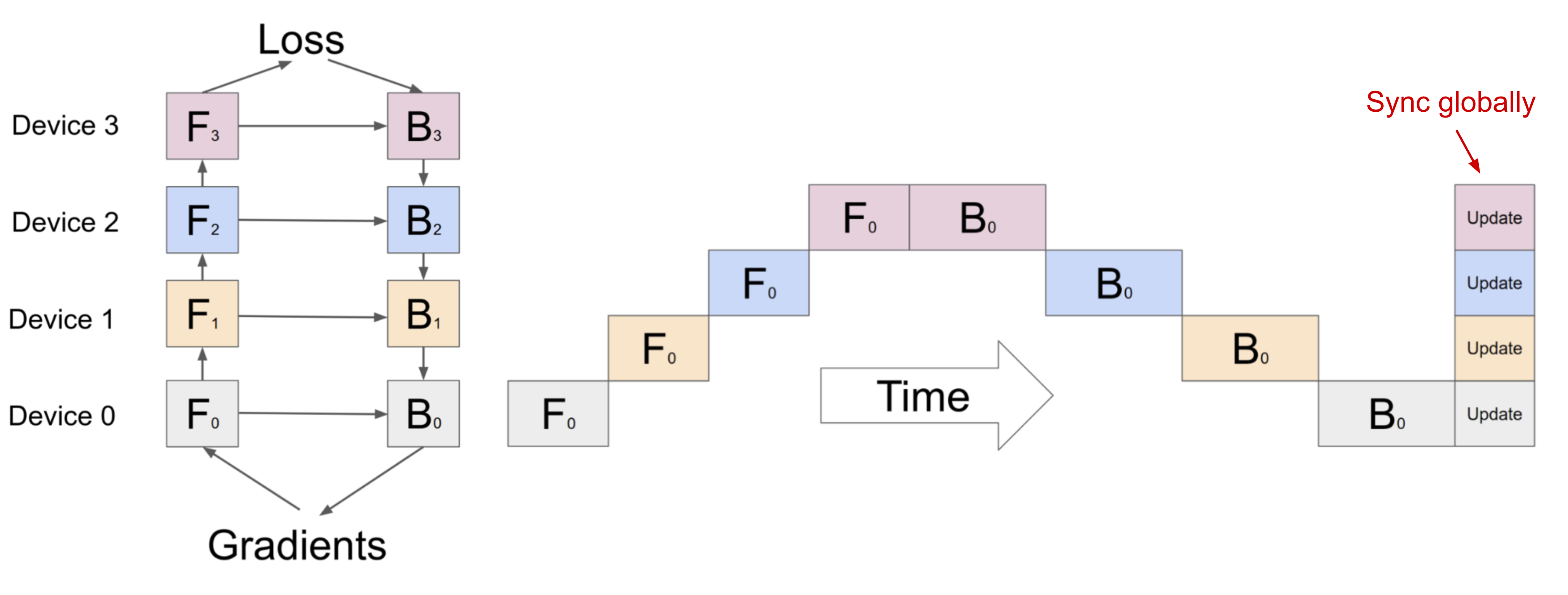
在 GPipe (Huang et al. 2019 ) 中，多个微批次的梯度被聚合并在最后同步应用。同步梯度下降保证了学习的一致性和效率，而不考虑工作节点的数量。如图 3 所示，仍然存在泡泡，但比图 2 中的要小得多。给定 $m$ 个均匀分割的微批次和 $d$ 个分区，假设每个微批次的前向和后向都需要一单位时间，泡泡的分数是：

$$ 1 - \frac{2md}{(2m + 2(d-1))d} = \frac{d-1}{m+d-1} $$

GPipe 论文观察到，如果微批处理的数量超过分区数量的 4 倍，即 $m > 4d$（当应用激活重计算时），泡沫开销几乎可以忽略不计。

图 3. GPipe 中带有 4 个微批处理和 4 个分区的流水线并行性示意图。GPipe 在每个批处理结束时，跨设备同步地聚合并更新梯度。（图片来源：Huang et al. 2019 ）

尽管如果模型参数没有在工作人员之间均匀分布，不能总是保证，但 GPipe 几乎可以实现与设备数量成线性比例的吞吐量增加。

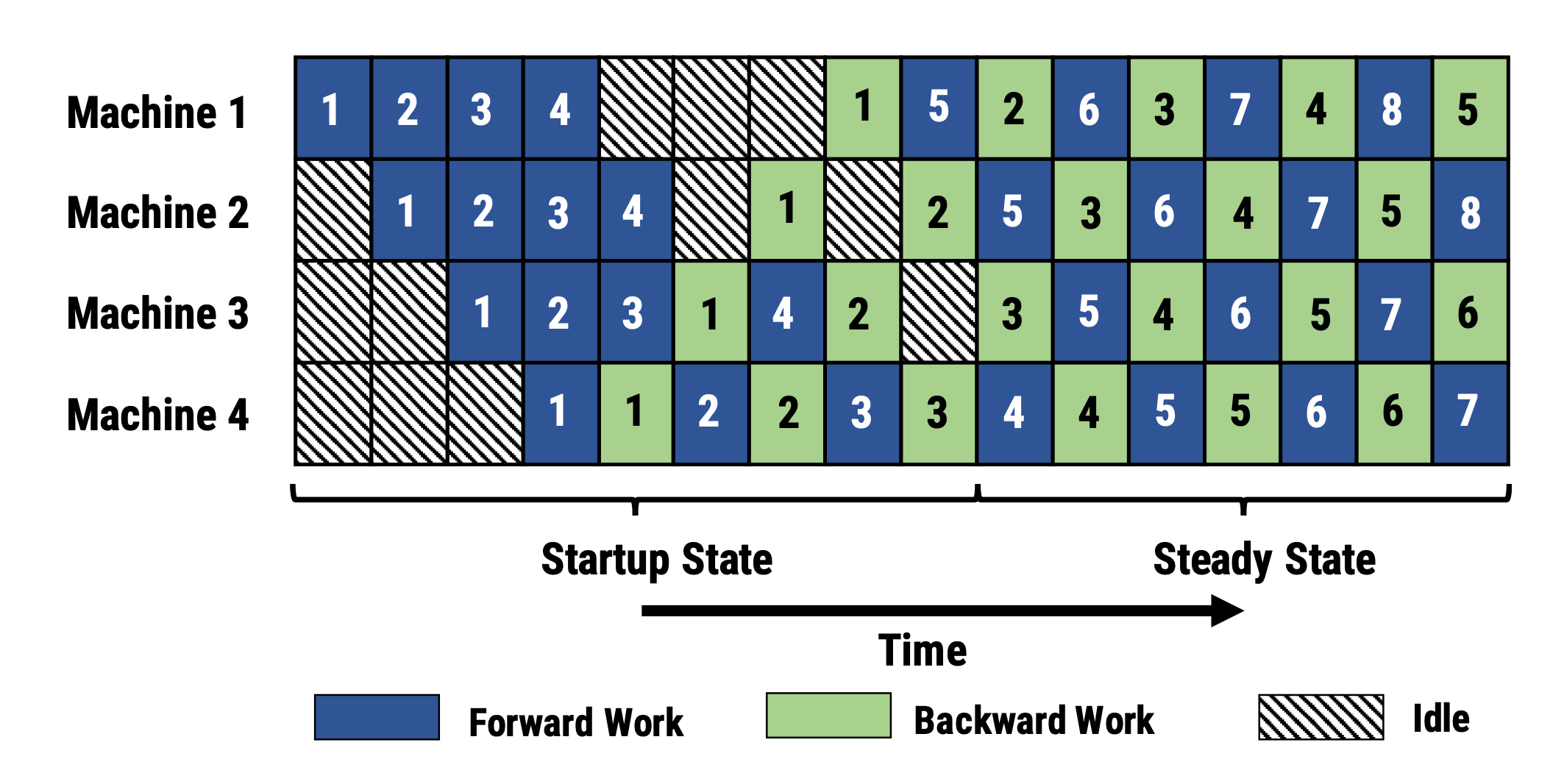
PipeDream（Narayanan et al. 2019 ）安排每个工作人员交替处理前向和反向传递（1F1B）。PipeDream 将每个模型分区命名为“阶段”，每个阶段工作人员可以有多个副本来运行数据并行性。在此过程中，PipeDream 使用确定性循环负载均衡策略在多个阶段的副本之间分配工作，以确保对同一小批量的前向和反向传递发生在同一副本上。

图 4. PipeDream 中的 1F1B 微批处理调度示意图。（图片来源：Harlap et al. 2018 ）

由于 PipeDream 不具有跨所有工作人员的批处理结束全局梯度同步，1F1B 的原生实现可能会导致一个微批处理的前向和反向传递使用不同版本的模型权重，从而降低学习效率。PipeDream 提出了几种设计来解决此问题：

权重缓存：每个工作人员跟踪几个模型版本，并确保在给定一个数据批处理时，前向和反向传递使用相同版本的权重。
垂直同步（可选）：模型权重的版本与激活和梯度一起在阶段工作人员之间流动。然后，计算采用从前一个工作人员传播的相应缓存版本。此过程保持了工作人员之间的版本一致性。请注意，它是异步的，与 GPipe 不同。

在训练运行开始时，PipeDream 首先分析模型中每层的计算内存成本和时间，然后优化将层分区到阶段的解决方案，这是一个动态编程问题。

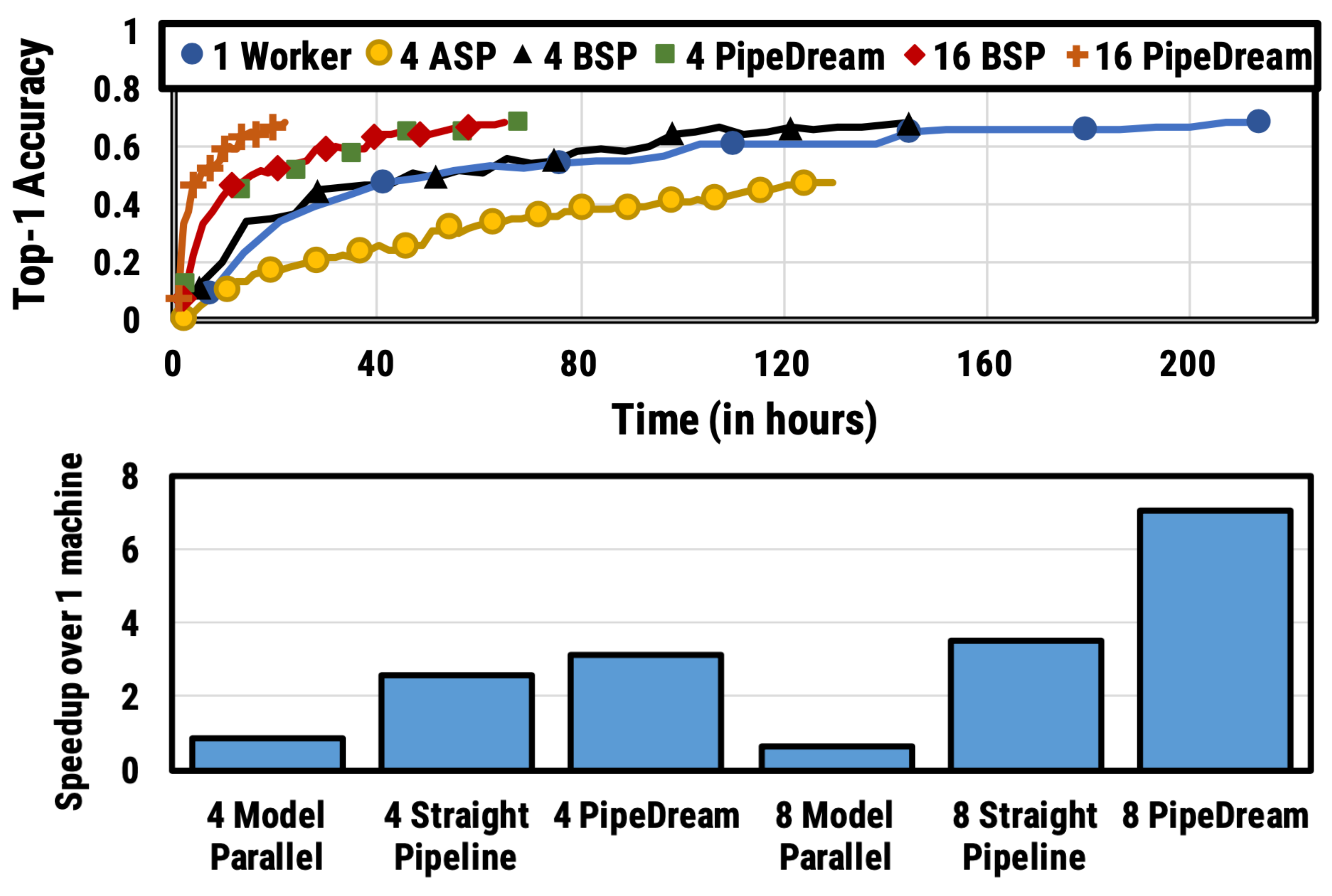
图 5. VGG16 在 ILSVRC12 上的结果。（上）准确性与时间。整数标记阶段工作人员的数量。ASP = 异步并行 & BSP = 批量同步并行。（下）不同并行配置的训练时间加速。直线管道指的是没有数据并行性的管道并行性。（图片来源：Harlap et al. 2018 ）

后来提出了两种 PipeDream 变体，以减少通过缓存模型版本的内存占用（Narayanan et al. 2021 ）。

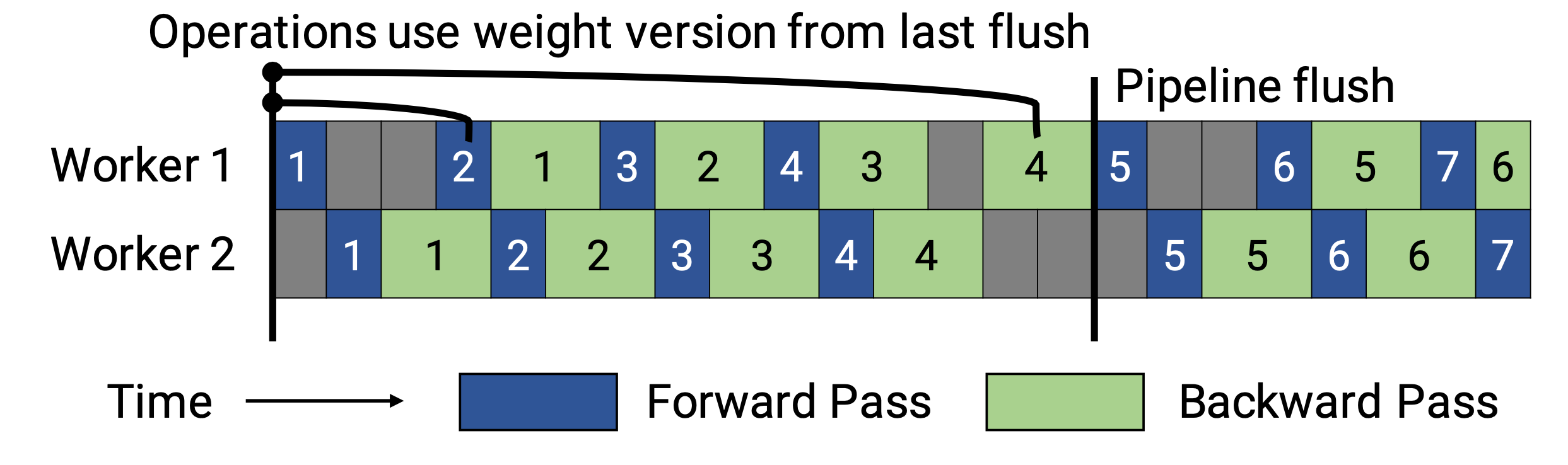
PipeDream-flush 定期添加了全局同步的管道刷新，就像 GPipe 一样。通过这种方式，它大大减少了内存占用（即只保留一个模型权重版本），牺牲了一点吞吐量。

图 6. PipeDream-flush 中的管道调度示意图。（图片来源：(Narayanan et al. 2021 )

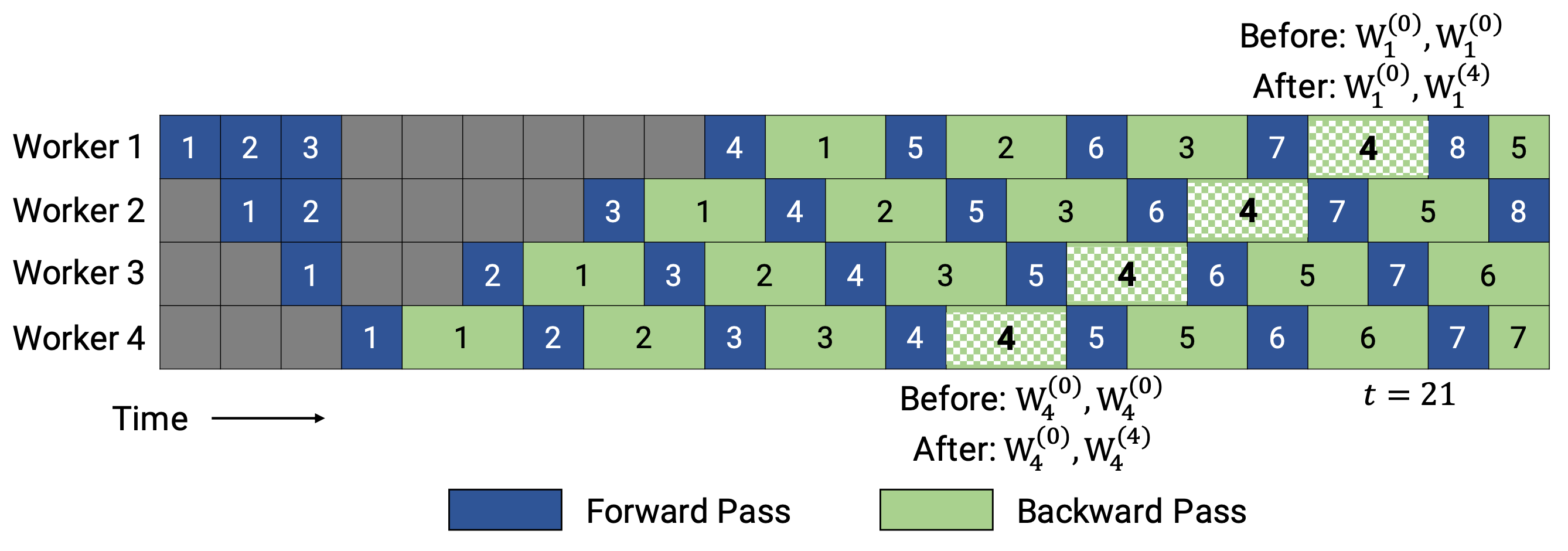
PipeDream-2BW 只保留两个版本的模型权重，其中 “2BW” 是 “双缓冲权重” 的缩写。它每隔 $k$ 微批处理生成一个新的模型版本，$k$ 应大于管道深度 $d$，即 $k > d$。新更新的模型版本不能立即完全替换旧版本，因为一些剩余的反向传递仍然依赖于旧版本。总的来说，只需保存两个版本，因此内存成本大大减少。

图 7. PipeDream-2BW 中的管道调度示意图。（图片来源： (Narayanan et al. 2021 )

张量并行性

模型并行和流水线并行都是垂直切分模型。但另一方面，我们可以将一个张量运算的计算过程横向切分到多个设备上，这被称为 张量并行性（TP）。

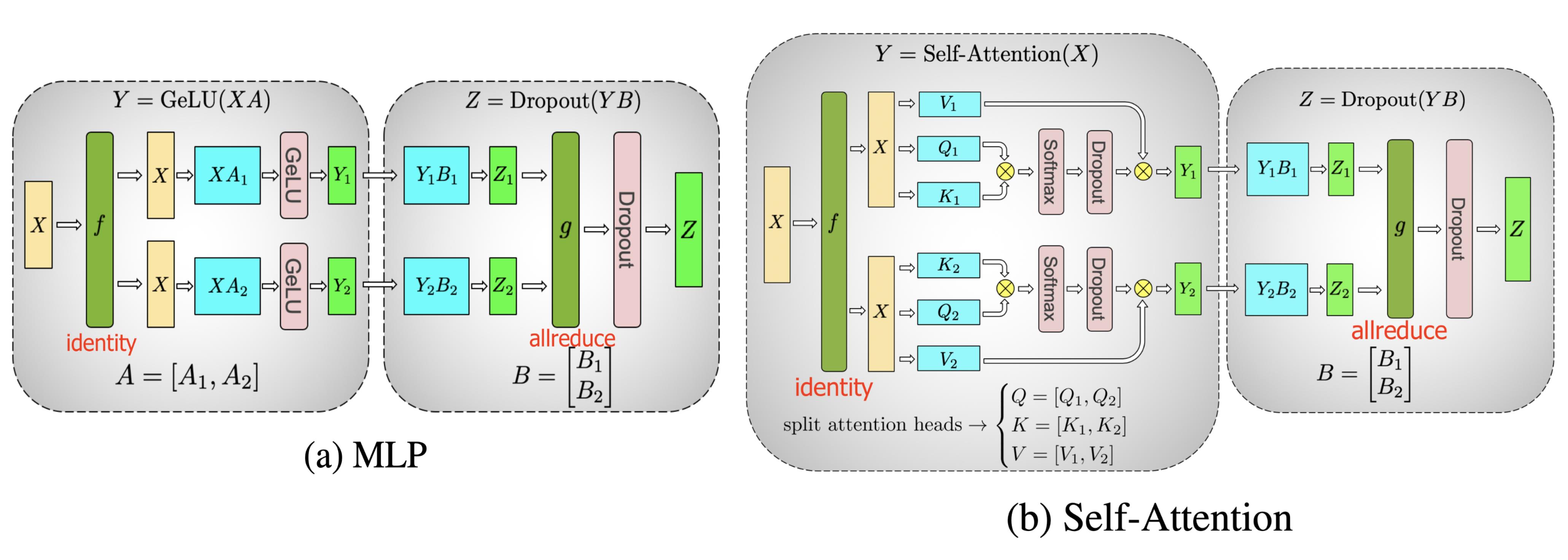
以现在广泛使用的 Transformer 为例。Transformer 模型主要由多层 MLP 和自注意力模块组成。Megatron-LM (Shoeybi 等人，2020 )采用了一种简单的方法来并行化 MLP 和自注意力层内的计算。

Transformer 中的 MLP 层包含了一个 GEMM（通用矩阵乘法）操作，接着是一个非线性的 GeLU 传递函数。我们按列切分权重矩阵 $A$：

$$ \begin{aligned} \text{切分 } A &= [A_1, A_2] \ Y &= \text{GeLU}(XA) \ [Y_1, Y_2] &= [\text{GeLU}(XA_1), \text{GeLU}(XA_2)] \end{aligned} $$

注意力模块按照上述切分方式并行运行 GEMM，对 query（$Q$）、key（$K$）和 value（$V$）权重进行计算，然后再通过另一个 GEMM 将它们组合起来，以产生注意力头结果。

$$ \text{Attention}(X, Q, K, V) = \text{softmax}\left(\frac{(XQ) (XK)^\top}{\sqrt{d\_k}}\right) XV $$

图 8. Megatron-LM 中提出的针对关键 Transformer 组件的张量并行性示意图。（图片来源：Shoeybi 等人，2020 ）

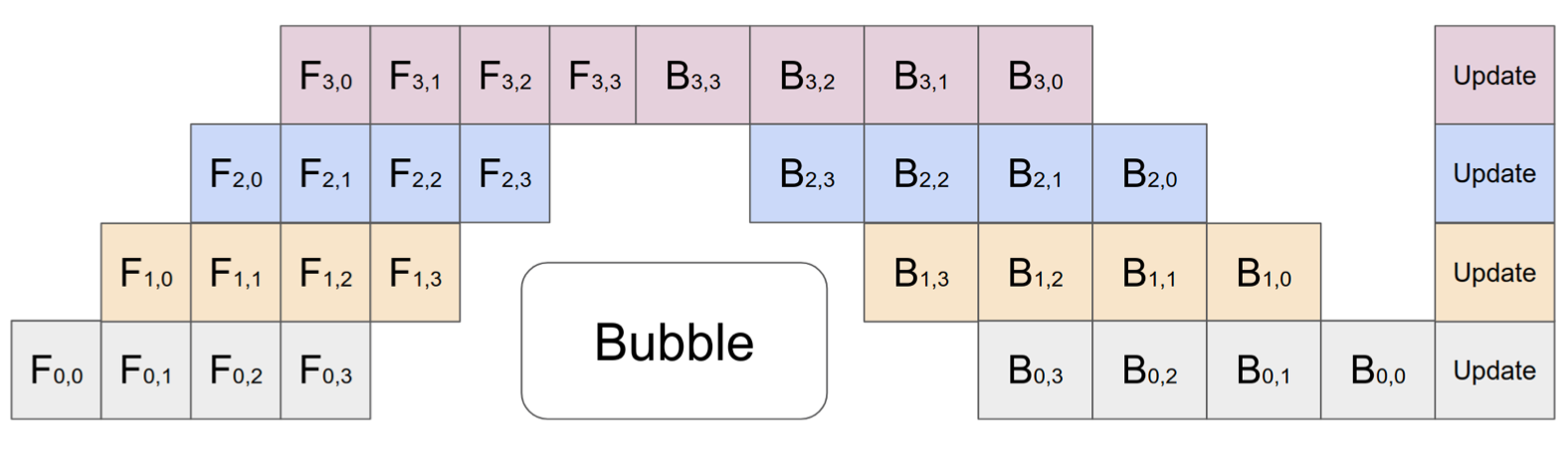
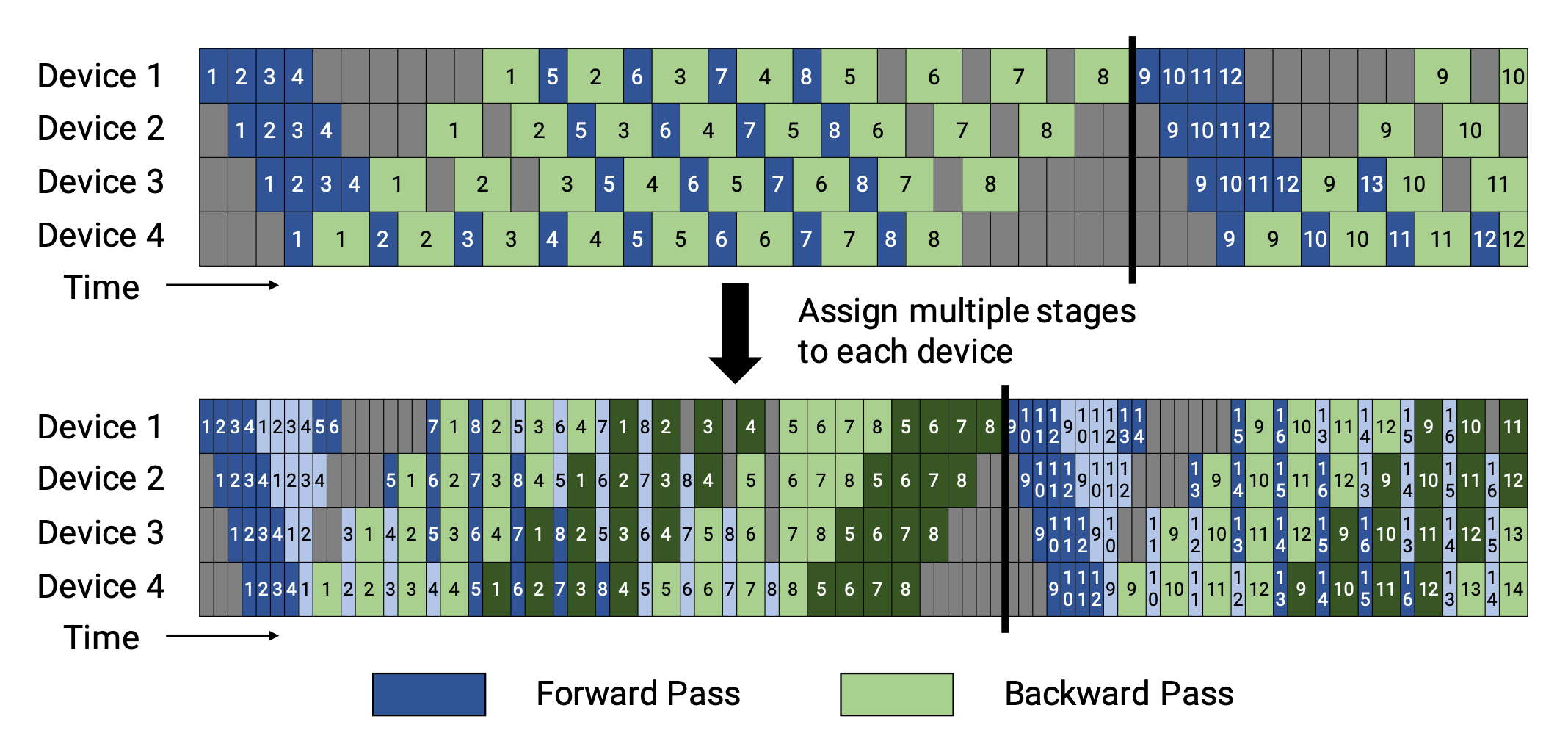
Narayanan 等人（2021）将流水线、张量和数据并行结合了新的流水线调度策略，将其命名为 PTD-P。与仅将连续层集（“模型块”）放置在一个设备上不同，每个工作器都可以被分配多个较小的连续层子集的块（例如，设备 1 有层 1、2、9、10；设备 2 有层 3、4、11、12；每个设备都有两个模型块）。一个批次中的微批次数量应该能够被工作器数量（$m % d = 0$）整除。如果每个工作器有 $v$ 个模型块，与 GPipe 调度相比，流水线泡沫时间可以减少 $v$ 倍。

图 9.（顶部）默认的 1F1B 流水线调度，如 PipeDream-flush 中所示。（底部）交错的 1F1B 流水线调度。第一模型块颜色较深，第二模型块颜色较浅。（图片来源：Narayanan 等人，2021 ）

专家混合 (MoE)

近期，专家混合 (Mixture-of-Experts, MoE) 方法吸引了许多关注，研究人员（主要来自 Google）尝试着推动模型大小的极限。这个想法的核心是集成学习：多个弱学习器的组合可以产生一个强学习器！

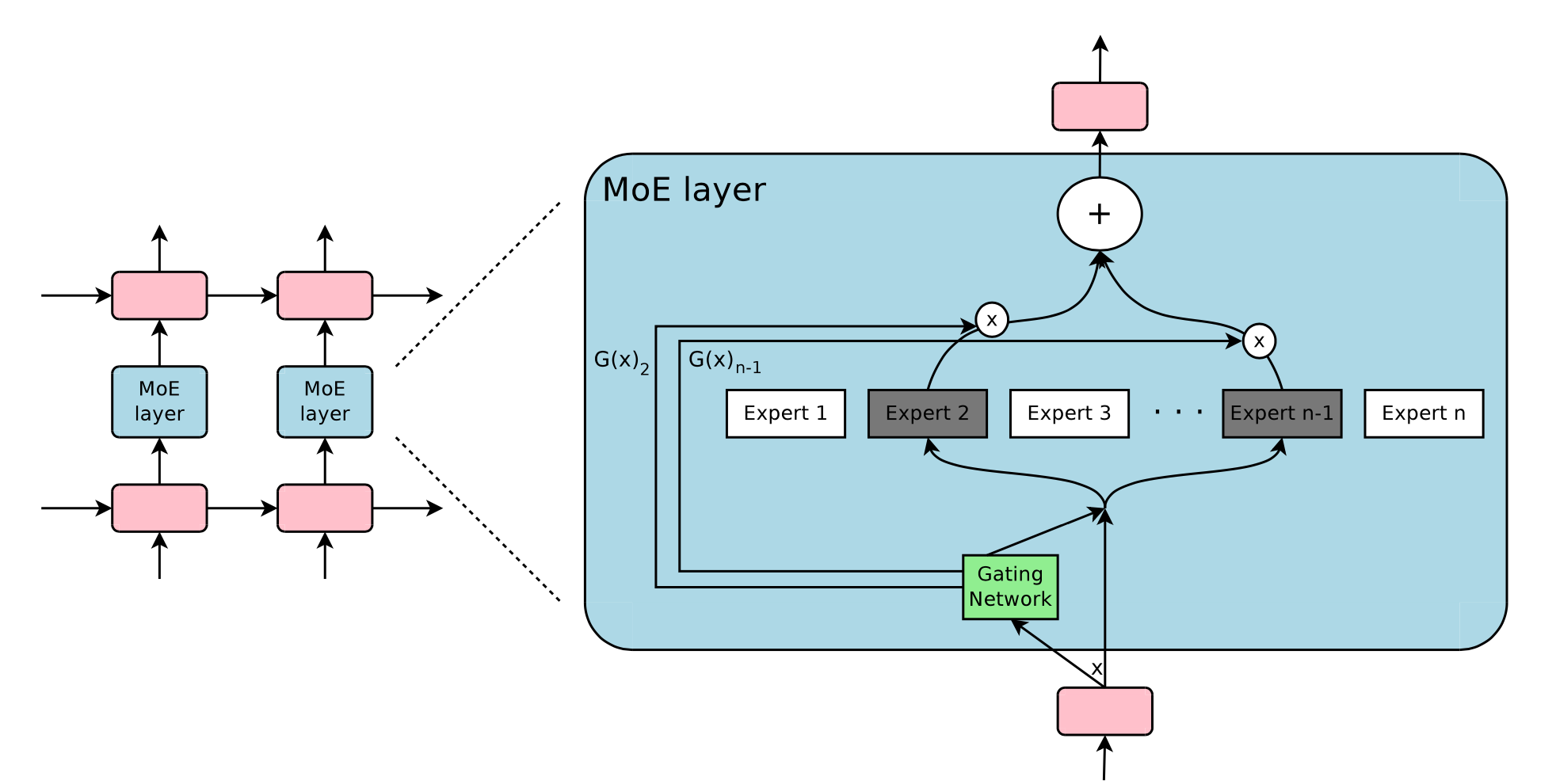
在一个深度神经网络中，可以通过与多个专家连接的门控机制来实现集成（Shazeer et al., 2017 ）。门控机制控制着网络的哪个子集（例如，哪些专家）应该被激活以产生输出。该论文将其命名为“稀疏门控专家混合” (MoE) 层。

准确地说，一个 MoE 层包含

$n$ 个前馈网络作为专家 ${E_i}^n_{i=1}$
一个可训练的门控网络 $G$，用于学习 $n$ 个专家上的概率分布，以便将流量路由到一些选定的专家。

根据门控输出，不是每个专家都必须被评估。当专家数量太大时，我们可以考虑使用两级层次的 MoE。

图 10. 专家混合（MoE）层的示意图。门控网络选中并激活了 $n$ 个专家中的 2 个。（图片来源：Shazeer et al., 2017 ）

一个简单的 $G$ 选择是将输入与一个可训练的权重矩阵 $G_g$ 相乘，然后进行 softmax：$G_\sigma(x) = \text{softmax}(x W_g)$。然而，这会产生一个密集的控制向量用于门控，并且不能节省计算资源，因为我们只有当 $G^{(i)}(x)=0$ 时才不需要评估一个专家。因此 MoE 层只保留了前 $k$ 个值。它还将可调的高斯噪声添加到 $G$ 中以改善负载平衡。这个机制被称为 噪音 top-k 门控。

$$ \begin{aligned} G(x) &= \text{softmax}(\text{topk}(H(x), k)) \ H^{(i)}(x) &= (xW_g)^{(i)} + \epsilon \cdot \text{softplus}((xW_\text{noise})^{(i)} ); \quad \epsilon \sim \mathcal{N}(0, \mathbf{1}) \ \text{topk}^{(i)}(v, k) &= \begin{cases} v^{(i)} & \text{if }v^{(i)}\text{ is in the top }k\text{ elements of }v \ -\infty & \text{otherwise} \end{cases} \end{aligned} $$

其中上标 $v^{(i)}$ 表示向量 $v$ 的第 i 维。函数 $\text{topk}(., k)$ 通过将其他维度设置为 $-\infty$ 来选择最高值的前 $k$ 维。

为了避免门控网络可能一直偏爱几个强专家的自强化效应，Shazeer et al. (2017) 提出了通过额外的重要性损失来鼓励所有专家具有相同权重的软约束。它相当于每个专家的批量平均值的变异系数的平方。

$$ L_\text{aux} = w_\text{aux} \cdot \text{CV}(\sum_{x \in X} G(x))^2 $$

其中 $ \text{CV}$ 是变异系数，损失权重 $w_\text{aux}$ 是一个要调整的超参数。

由于每个专家网络只能获得一部分训练样本（“缩小的批处理问题”），我们应该尽量使用尽可能大的批大小在 MoE 中。然而，它受到 GPU 内存的限制。可以应用数据并行和模型并行来提高吞吐量。

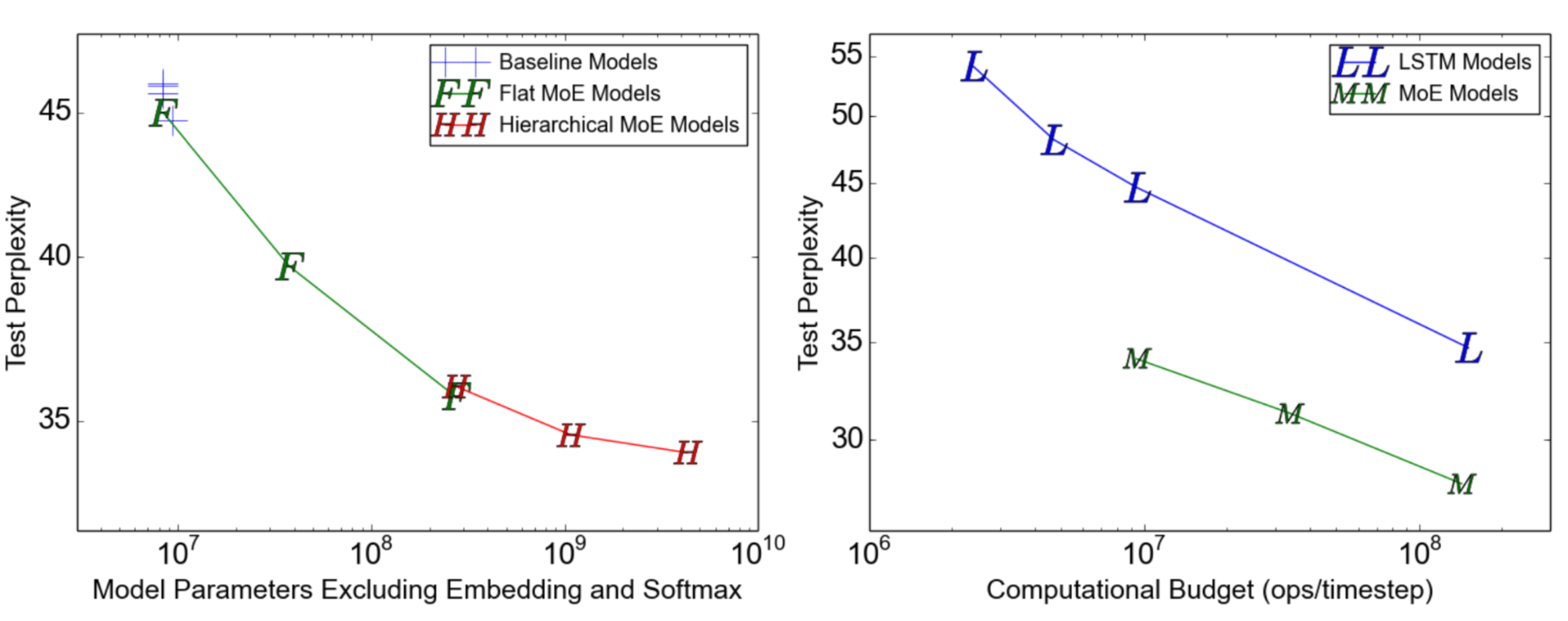
图 11. 在 1-Billion-Word 语言建模基准测试上的困惑度测试。（左图）模型容量从左到右递增，包含 4、32、256、256、1024 和 4096 个专家。（右图）在不同计算预算下，4 十亿参数的 MoE 模型的性能，这是左图中最大的一个模型。（图片来源：Shazeer et al., 2017 ）

GShard (Lepikhin et al., 2020 ) 通过切片技术，将 MoE 变换器模型的参数量扩展到 6000 亿。MoE 变换器将每隔一个前馈层替换为 MoE 层。切片的 MoE 变换器 只有 MoE 层是跨多台机器切片的，而其他层则简单地复制了。

GShard 中对门控函数 $ G $ 的几个改进设计包括：

专家容量：通过一个专家的令牌数量不应超过一个名为“专家容量”的阈值。如果一个令牌被路由到已经达到其容量的专家，该令牌将被标记为“溢出”，并且门控输出将变为零向量。
本地组调度：令牌被均匀划分为多个本地组，并在组级别上执行专家容量。
辅助损失：其动机与原始 MoE 辅助损失相似。他们添加了一个辅助损失，以最小化路由到每个专家的数据分数的均方。
随机路由：第二好的专家被选中的概率与其权重成正比；否则，GShard 遵循随机路由，以增加一些随机性。

图 12. GShard 中带有辅助损失的组级别 top-2 门控机制的伪代码。（图片来源：Lepikhin et al., 2020 ）

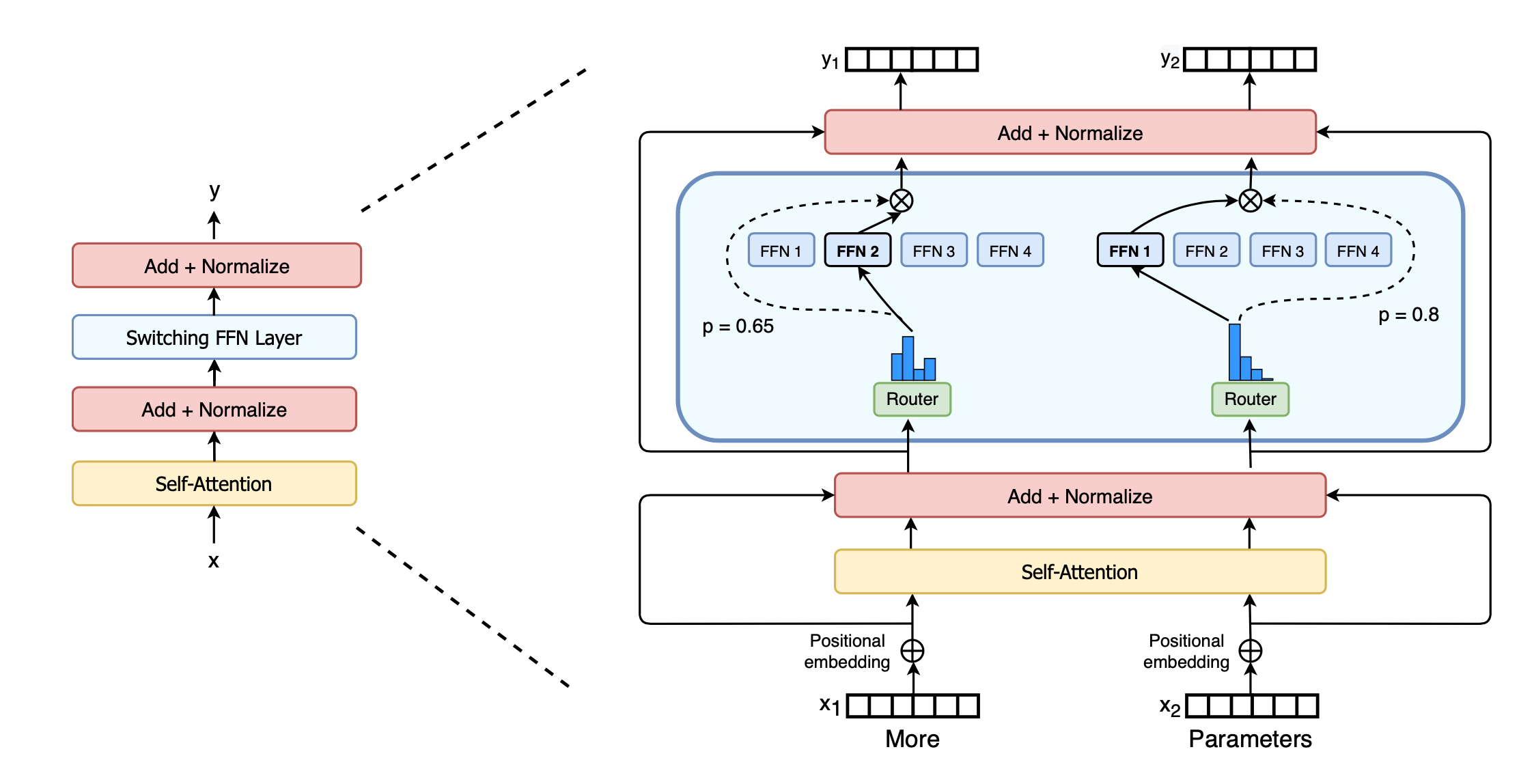
Switch Transformer (Fedus et al. 2021 ) 通过将密集前馈层替换为 稀疏开关 FFN 层，将模型大小扩展到数万亿参数(!!)，在该层中，每个输入只路由到一个专家网络。负载平衡的辅助损失为 $ \text{loss}_{\text{aux}} = w_{\text{aux}} \sum_{i=1}^n f_i p_i $，其中 $ n $ 是专家的数量，$ f_i $ 是路由到第 $ i $ 个专家的令牌分数，$ p_i $ 是由门控网络预测的第 $ i $ 个专家的路由概率。

图 13. Switch Transformer。稀疏开关 FFN 层位于蓝色框内。（图片来源：Fedus et al. 2021 ）

为了提高训练稳定性，Switch Transformer 采用了以下设计：

选择性精度。他们表明，只将模型的局部部分选择性地转换为 FP32 精度可以提高稳定性，同时避免了 FP32 张量的昂贵通信成本。FP32 精度仅用于路由器函数的主体内，结果重新转换为 FP16。
较小的初始化。权重矩阵的初始化是从截断正态分布中采样的，均值 $ \mu = 0 $，标准差 $ \sigma = \sqrt{s/n} $。他们还建议将变换器初始化比例参数 $ s=1 $ 减小到 $ s=0.1 $。
使用更高的专家退出率。微调通常适用于小数据集。为了避免过拟合，他们在每个专家内大幅增加了退出率。有趣的是，他们发现在所有层增加退出率会导致性能下降。在论文中，他们在非专家层使用了 0.1 的退出率，但在专家 FF 层内使用了 0.4 的退出率。

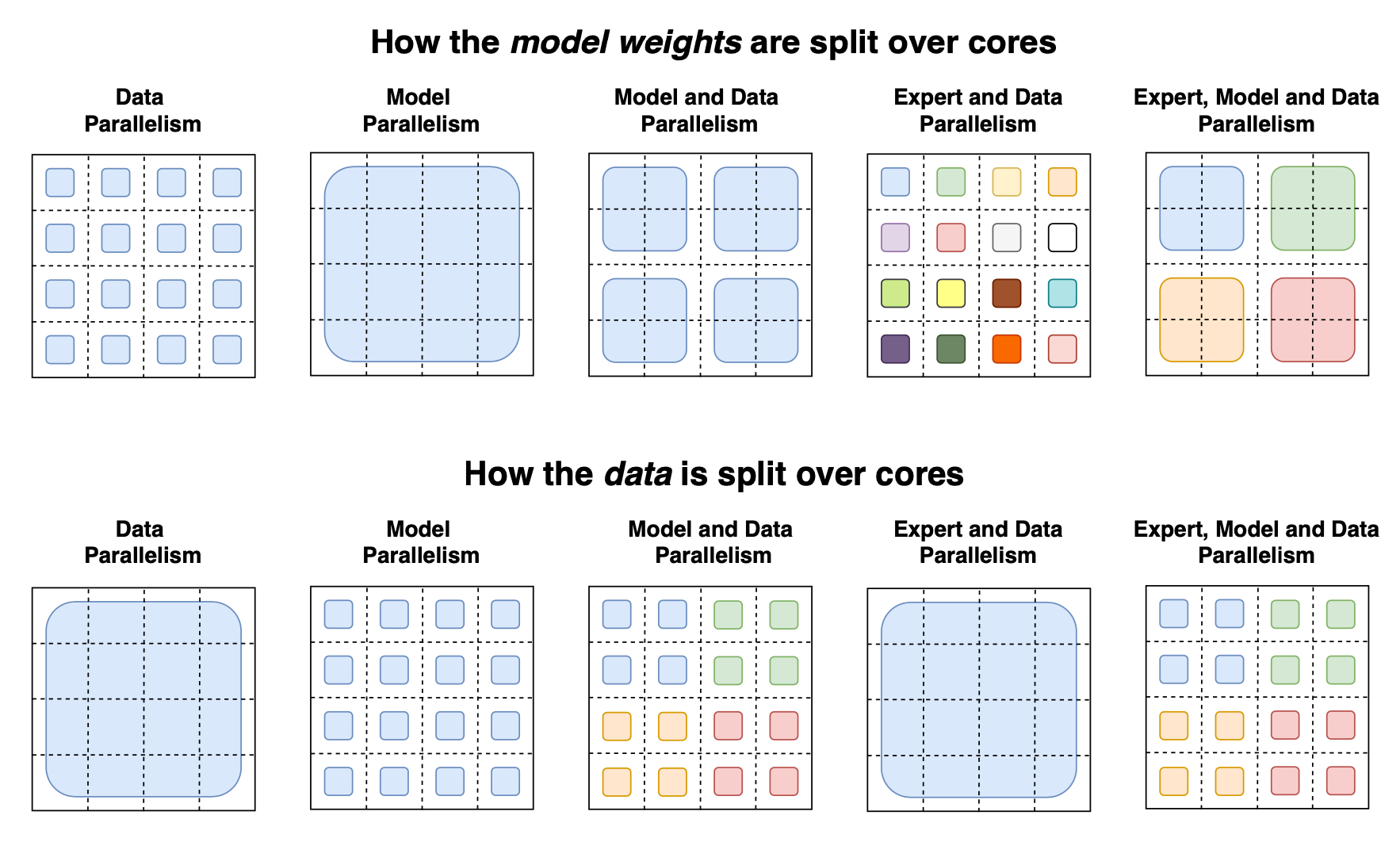
Switch Transformer 论文总结了用于训练大型模型的不同数据和模型并行策略，并提供了一个很好的示意图：

图 14. 关于如何（顶部）模型权重和（底部）数据在多个 GPU 核心上分割的各种并行策略的示意图。在顶行，每种颜色代表一个唯一的权重矩阵。在底行，不同的颜色表示不同的令牌集。 (图片来源：Fedus et al. 2021 )

GShard top-2 和 Switch Transformer top-1 都依赖于 令牌选择，其中每个令牌选择最好的一个或两个专家来进行路由。它们都采用了一个辅助损失来鼓励更均衡的负载分配，但不能保证最佳性能。此外，专家的容量限制可能会导致令牌的浪费，因为如果一个专家达到其容量限制，令牌将被丢弃。

专家选择 (EC) (Zhou et al. 2022 ) 的路由使每个专家能够选择 top-$k$ 令牌。这样，每个专家自然地保证了固定的容量，每个令牌可能会被路由到多个专家。EC 能够实现完美的负载平衡，并且已显示出能够将训练收敛速度提高 2 倍。

给定 $e$ 个专家和一个输入矩阵 $X \in \mathbb{R}^{n \times d}$，通过计算得到令牌到专家的亲和得分：$$ S = \text{softmax}(X \cdot W_g), \text{其中 } W_g \in \mathbb{R}^{d \times e}, S \in \mathbb{R}^{n \times e} $$

令牌到专家的分配由三个矩阵表示，$I, G \in \mathbb{R}^{e\times k}$ 和 $P \in \mathbb{R}^{e \times k \times n}$。$I[i,j]$ 标注了由第 $i$ 个专家选择的第 $j$ 个令牌。门控矩阵 $G$ 存储了选定令牌的路由权重。$P$ 是 $I$ 的 one-hot 版本，用于产生门控 FFN 层的输入矩阵 ($P \cdot X \in \mathbb{R}^{e \times k \times d}$)。$$ G, I = \text{top-k}(S^\top, k) \quad P = \text{one-hot}(I) $$

专家选择路由探索的一个正则化是限制每个令牌的最大专家数量。

$$ \begin{aligned} & \max_A \langle S^\top, A\rangle + \lambda H(A) \\ \text{s.t.} & \forall i: \sum_{j’} A[i, j’] = k, \quad \forall j: \sum_{i’} A[i’, j] \leq b, \quad \forall i,j: 0 \leq A[i,j] \leq 1 \end{aligned} $$

其中，每个条目 $A[i,j]$ 在 $A \in \mathbb{R}^{e \times n}$ 中标记第 $i$ 个专家是否选择第 $j$ 个令牌。解决这个问题并非易事。论文使用了 Dykstra 的算法进行了一系列多次迭代计算步骤。在实验中，限制专家选择导致微调性能略有下降。

参数 $k$ 由 $k=nc/e$ 确定，其中 $n$ 是一个批次中的总令牌数，$c$ 是表示一个令牌平均使用的专家数量的容量因子。论文在大多数实验中使用了 $c=2$，但是 $c=1$ 的 EC 仍然优于 top-1 令牌选择门控。有趣的是，$c=0.5$ 仅对训练性能造成了边际损害。

EC 的一个大缺点是当批大小太小时，它不起作用，也不适用于自回归文本生成，因为它需要知道未来的令牌来进行 top-$k$ 选择。

$$ \begin{aligned} & \max_A \langle S^\top, A\rangle + \lambda H(A) \\ \text{s.t.} & \forall i: \sum_{j'} A[i, j'] = k,\quad \forall j: \sum_{i'} A[i', j] \leq b,\quad \forall i,j: 0 \leq A[i,j] \leq 1 \end{aligned} $$

每个条目 $A[i,j]$ 标记在 $A \in \mathbb{R}^{e \times n}$ 中。是否 $i$-位专家选择了 $j$-位令牌。解决这个问题并非易事。该论文使用了 Dykstra 的算法，它通过运行多个迭代计算步骤的序列来进行。在实验中，限制专家选择会轻微降低微调性能。

参数 $k$ 由 $k=nc/e$ 确定，其中 $n$ 是一个批次中的令牌总数，$c$ 是一个表示由一个令牌使用的专家平均数的容量因子。在大多数实验中，论文使用了 $c=2$，但是即使 $c=1$，EC 仍然优于顶部 -1 令牌选择门控。有趣的是，$c = 0.5$ 只会对训练性能造成微小的伤害。

EC 的一个大缺点是，当批量太小时它不起作用，对于自回归文本生成也是如此，因为它需要知道未来的令牌来进行顶部-$k$ 选择。

其他节省内存的设计

CPU 卸载

当 GPU 内存已满时，一种选择是暂时将未使用的数据卸载到 CPU，并在稍后需要时读回它们（Rhu 等人，2016 ）。CPU 卸载的想法很简单，但由于它使训练时间变慢，所以近年来较为不流行。

激活重计算

激活重计算（也称为 “激活检查点” 或 “梯度检查点”；Chen 等人，2016 ）是一种聪明而简单的想法，它以计算时间为代价来减少内存占用。它将训练一个 $ℓ$ 层深神经网络的内存成本降低到 $O(√ℓ)$，每个批次只额外消耗一个前向传递计算。

假设我们将一个 $ℓ$-层网络均匀划分为 $d$ 个分区。只有在分区边界处的激活被保存和在工作者之间传输。在分区内的层上的中间激活仍然需要计算梯度，所以它们在反向传递期间被重新计算。使用激活重计算，训练 $M(ℓ)$ 的内存成本为：

$$[ M(ℓ) =\max_{i=1,\dots,k} \underbrace{\text{cost-of-one-partition}(i)}_{\text{cost of back-propagation on the i-th partition}} + \underbrace{O(d)}_{\text{store intermediate outputs}} = O(\frac{ℓ}{d}) + O(d) ] $$

在 $d=\sqrt{\ell}$ 处的最小成本是 $O(\sqrt{\ell})$。

激活重计算技巧可以使内存成本相对于模型大小呈亚线性。

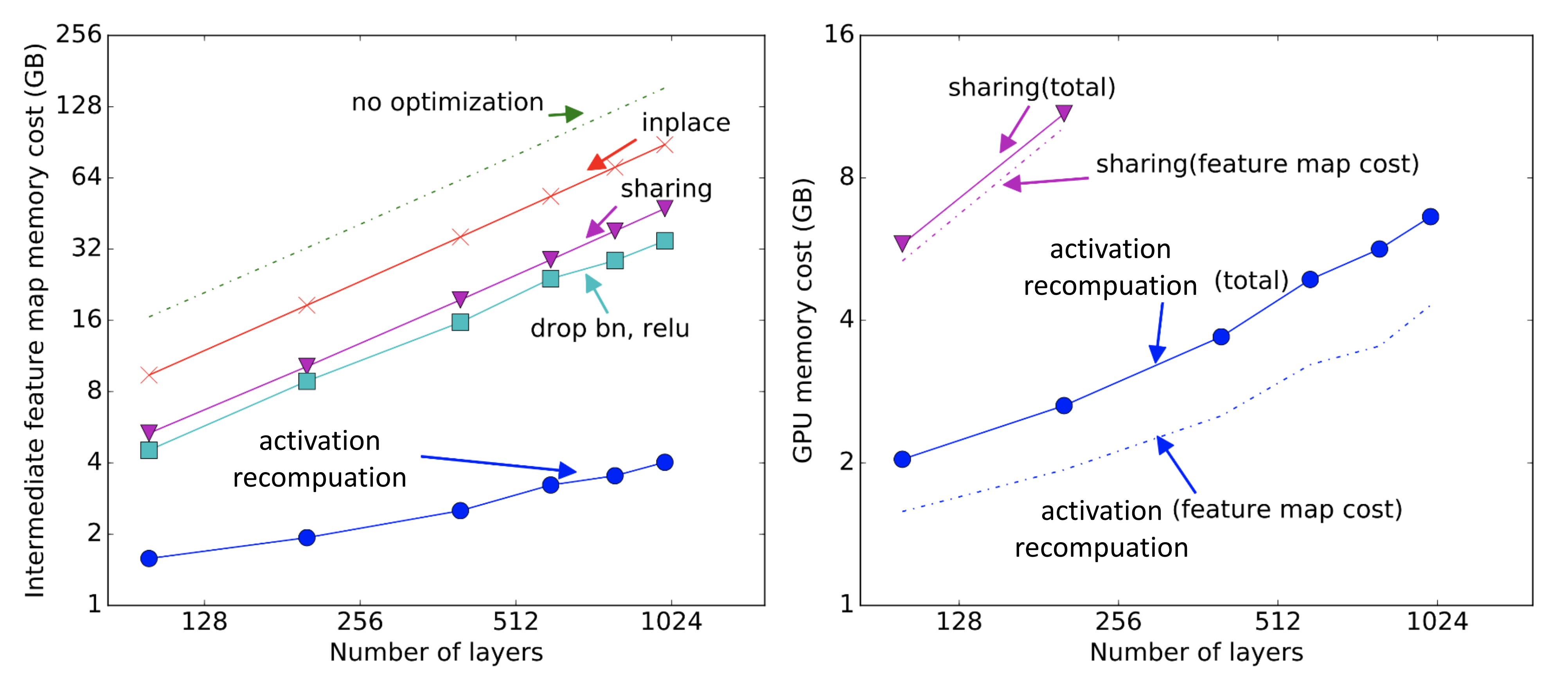
图 15. 不同节省内存算法的内存成本。 [Sharing]{.ul}：在不再需要时，由中间结果使用的内存被回收。 [Inplace]{.ul}：直接将输出保存到输入值的内存中。 (图片来源：Chen 等人，2016 )

混合精度训练

Narang & Micikevicius 等人 (2018) 提出了一种使用半精度浮点数（FP16）训练模型而不损失模型准确性的方法。

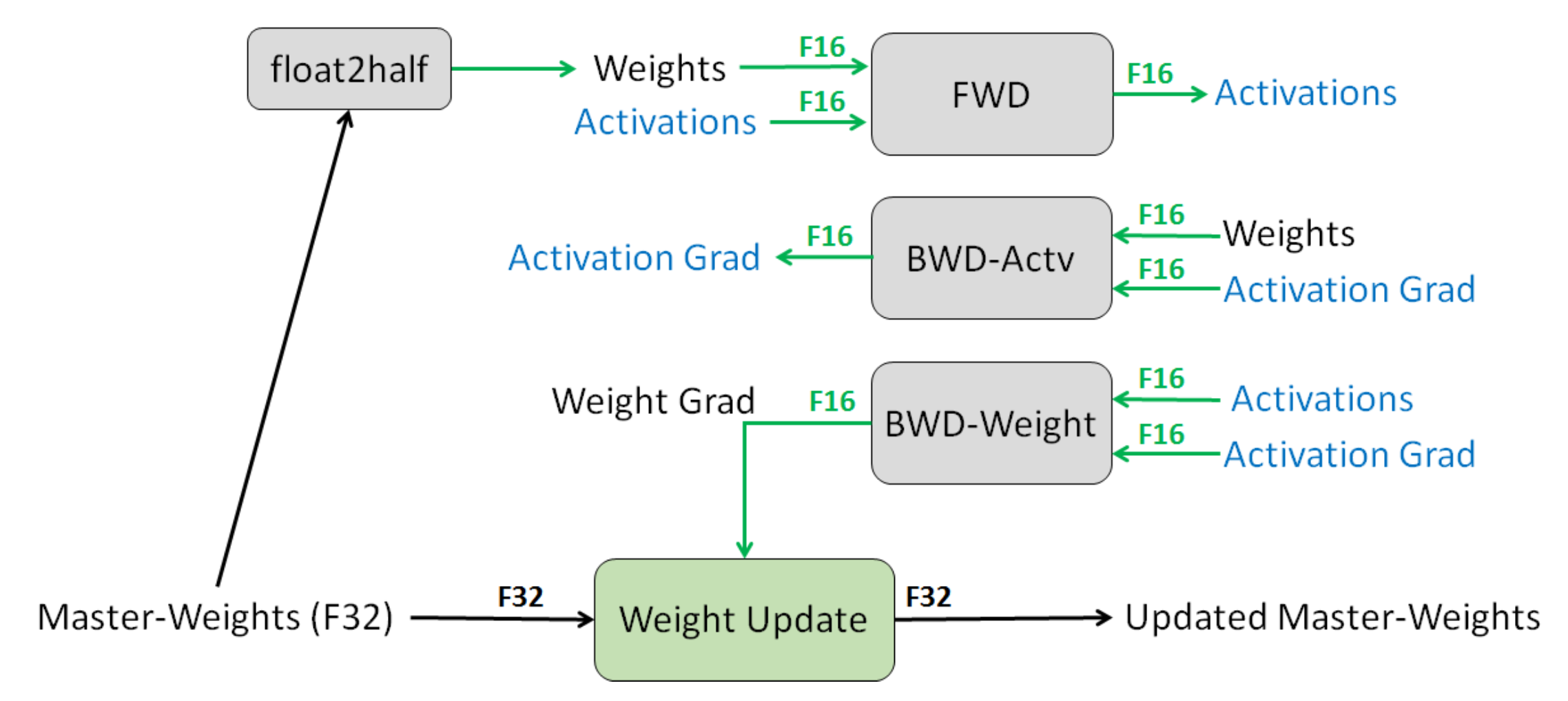
图 16. 一层混合精度训练的过程。（图片来源：Narang & Micikevicius 等人 2018 ）

为避免在半精度下丢失关键信息的三种技术：

全精度主权重副本。保持模型权重的全精度（FP32）副本，以累积梯度。这些数字会在前向和后向传递时四舍五入到半精度。动机是每次梯度更新（即，梯度乘以学习率）可能太小，无法完全包含在 FP16 范围内（例如，$2^{-24}$ 在 FP16 中变为零）。
损失缩放。放大损失以更好地处理具有小幅度的梯度（参见图 16）。放大梯度有助于将它们移至可表示范围的右侧（包含较大值）的更大部分，以保留否则会丢失的值。
算术精度。对于常见的网络算术（例如，向量点积，通过求和向量元素进行缩减），我们可以在 FP32 中累积部分结果，然后在保存到内存之前将最终输出保存为 FP16。点式操作可以在 FP16 或 FP32 中执行。

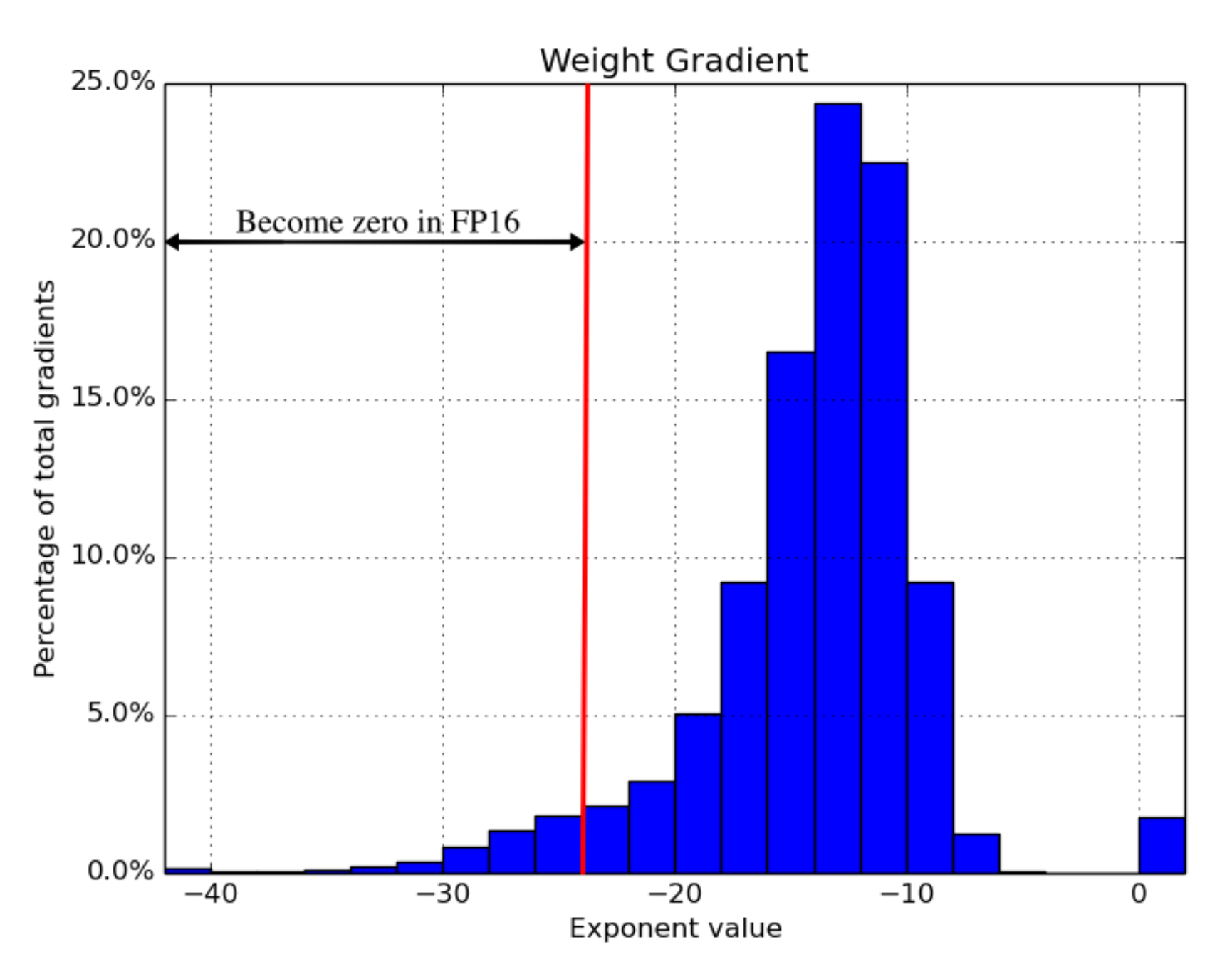
图 17. 全精度梯度的直方图。一旦模型切换到 FP16，直至 $2^{-24}$ 的左侧部分将被清零。（图片来源：Narang & Micikevicius 等人 2018 ）

在他们的实验中，对于某些网络（例如，图像分类，Faster R-CNN）不需要损失缩放，但对于其他网络（例如，Multibox SSD，大型 LSTM 语言模型）则是必需的。

压缩

中间结果通常会消耗大量内存，尽管它们只在一个前向传递和一个后向传递中需要。在这两种使用之间存在明显的时间间隔。因此 Jain 等人 (2018) 提出了一种数据编码策略，以在第一次传递的第一次使用后压缩中间结果，然后在稍后的反向传播中对其进行解码。

他们的系统 Gist 包含两种编码方案：特定于层的无损编码；重点关注 ReLU-Pool（“二值化”）和 ReLU-Conv（“稀疏存储和密集计算”）模式。积极的有损编码；使用延迟精度降低（DPR）。他们观察到，特征图的第一次直接使用应保持高精度，但第二次使用可以容忍较低的精度。

实验表明，Gist 可以在 5 个 SOTA 图像分类 DNN 中将内存成本减少 2 倍，平均仅有 4% 的性能开销，平均减少 1.8 倍。

内存高效优化器

优化器对内存的需求很高。以流行的 Adam 优化器为例，它内部需要维护动量和方差，其规模与梯度和模型参数相同。突然间，我们需要保存模型权重的 4 倍内存。

为了减少内存占用，已经提出了一些优化器。例如，与 Adam 中存储完整动量和变化不同，Adafactor（Shazeer 等人，2018 ）只跟踪移动平均值的每行和每列总和，然后根据这些总和估算第二时刻。SM3（Anil 等人，2019 ）描述了一种不同的自适应优化方法，也大大减少了内存占用。

ZeRO（Zero Redundancy Optimizer，Rajbhandari 等人，2019 ）优化了用于训练大型模型的内存使用，基于对大型模型训练的两个主要内存消耗的观察：

大部分被 模型状态 占用，包括优化器状态（例如 Adam 的动量和方差）、梯度和参数。混合精度训练需要大量内存，因为优化器需要保留 FP32 参数和其他优化器状态的副本，除了 FP16 版本。
其余的被激活、临时缓冲区和不可用的碎片化内存（在论文中称为 残余状态）消耗。

ZeRO 结合了两种方法，ZeRO-DP 和 ZeRO-R。ZeRO-DP 是一种增强的数据并行性，以避免模型状态上的简单冗余。它通过动态通信时间表将优化器状态、梯度和参数分区到多个数据并行过程中，以最小化通信量。ZeRO-R 优化了残余状态的内存消耗，使用分区激活重计算、常量缓冲区大小和实时内存碎片整理。

引用

Cited as:

Weng, Lilian. (Sep 2021). How to train really large models on many GPUs? Lil’Log. https://lilianweng.github.io/posts/2021-09-25-train-large/ .

1
2
3
4
5
6
7
8


@article{weng2021large,
  title   = "How to Train Really Large Models on Many GPUs?",
  author  = "Weng, Lilian",
  journal = "lilianweng.github.io",
  year    = "2021",
  month   = "Sep",
  url     = "https://lilianweng.github.io/posts/2021-09-25-train-large/"
}