[January 10, 2023] · 31 min · Lilian Weng

2023-01-24 更新：增加了关于蒸馏 的小节

如今，大型 Transformer 模型已经成为主流，为各种任务创造了 SoTA (最先进的技术) 结果。它们功能强大但训练和使用的成本非常高。极高的推理成本，无论是在时间还是内存上，都成为了采用强大的 Transformer 来大规模解决实际任务的重大瓶颈。

**为什么大型 Transformer 模型的推理很困难？**除了 SoTA 模型的不断增大，还有两个主要因素导致了推理的挑战性（Pope et al. 2022 ）：

1. 大内存占用。在推理时，需要在内存中保留模型参数和中间状态。例如，
   • 在解码时间内，应将 KV 缓存存储在内存中；例如，对于批量大小为 512 和上下文长度为 2048，KV 缓存总计 3TB，这是模型大小的 3 倍(!)。
   • 来自注意机制的推理成本与输入序列长度呈二次关系。
2. 低并行性。推理生成以自回归方式执行，使解码过程难以并行化。

在这篇文章中，我们将探讨几种使 Transformer 推理更为高效的方法。其中一些是通用的网络压缩方法，而另一些是特定于 Transformer 架构的。

方法概览

通常，我们将以下内容视为模型推理优化的目标：

• 通过使用更少的 GPU 设备和更少的 GPU 内存来减小模型的内存占用；
• 通过降低所需的 FLOPs 数量来减少期望的计算复杂度；
• 减少推理延迟，使事务运行得更快。

可以使用几种方法来使推理在内存或/和时间上更便宜。

1. 应用各种 并行性，以便在大量 GPU 上扩展模型。模型组件和数据的智能并行性使得可以运行具有万亿参数的模型。
2. 内存 卸载，将暂时不用的数据卸载到 CPU，并在稍后需要时再读回。这有助于节省内存，但会导致更高的延迟。
3. 智能的批处理策略；例如，EffectiveTransformer 将连续序列打包在一起，以消除一个批次内的填充。
4. 网络 压缩 技术，如 剪枝、量化、蒸馏。较小尺寸的模型（无论是在参数计数还是位宽方面）应该需要较少的内存并运行得更快。
5. 针对目标模型架构的改进。许多 架构变更，尤其是对注意层的那些变更，有助于提高 Transformer 解码速度。

查看大型模型训练的前一篇文章 ，了解不同类型的训练并行性和包括CPU内存卸载在内的节省内存设计。本文侧重于网络压缩技术和针对 Transformer 模型的特定架构改进。

蒸馏

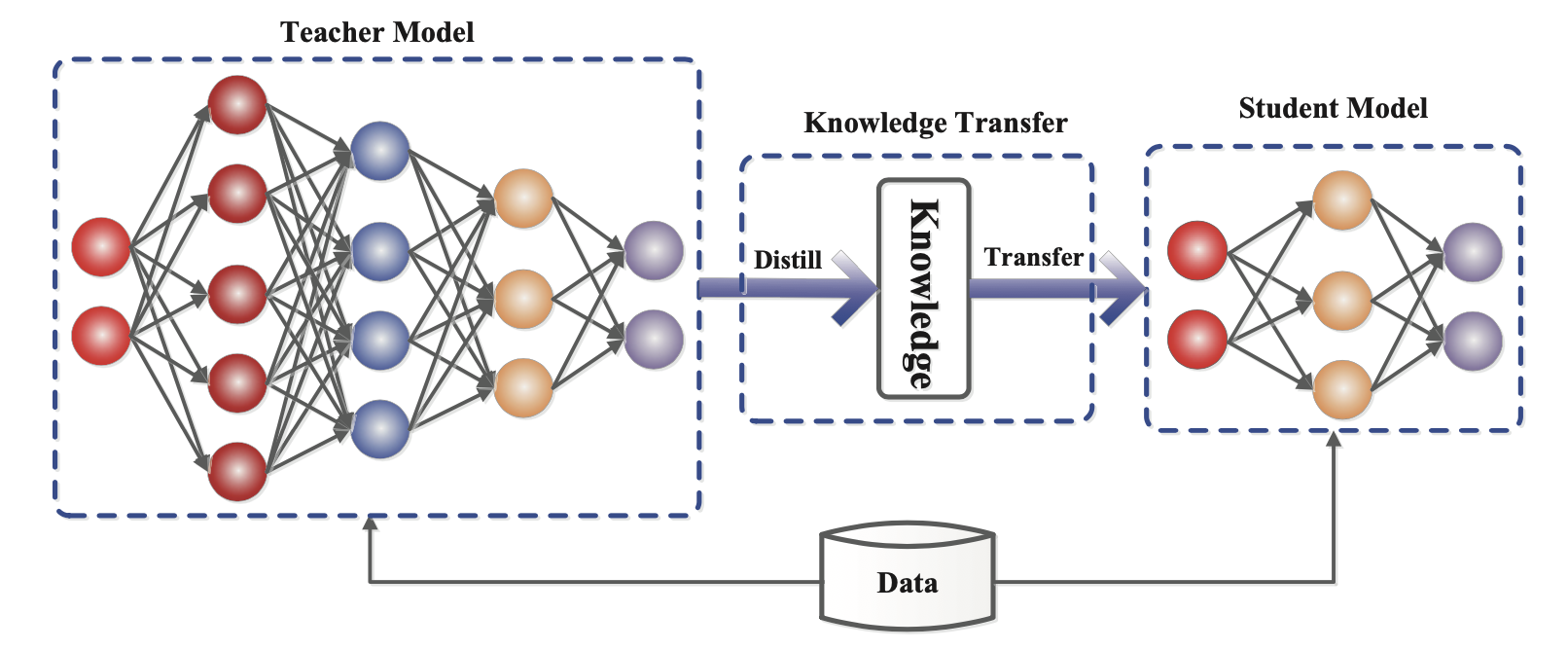
知识蒸馏 (KD; Hinton 等人 2015 , Gou 等人 2020 )是一种直接的方法，通过从预训练的昂贵模型（“教师模型”）中转移技能，构建一个更小、更便宜的模型（“学生模型”）来加速推理。对于如何构造学生架构几乎没有什么限制，只要与教师的输出空间匹配，以便构建适当的学习目标。

图 1. 教师-学生知识蒸馏训练的通用框架。(图片来源：Gou 等人 2020 )

给定一个数据集，学生模型通过蒸馏损失来模仿教师的输出。通常神经网络具有一个 softmax 层；例如，LLM 输出一个关于 token 的概率分布。让我们用 $\mathbf{z}_t$ 和 $\mathbf{z}_s$ 分别表示教师和学生模型在 softmax 之前的 logits 层。蒸馏损失 通过高温度 $T$ 最小化两个 softmax 输出之间的差异。当已知地面真实标签 $\mathbf{y}$ 时，我们可以将其与学生的软 logits 之间的监督学习目标结合起来，例如使用交叉熵。

其中，$\lambda$ 是一个用于平衡软和硬学习目标的超参数。对于 $\mathcal{L}_\text{distll}$，常见的选择是 KL 散度 / 交叉熵。

一个成功的早期尝试是 DistilBERT (Sanh 等人 2019 )，它能够在保持 BERT 在微调下游任务上 97% 的性能的同时，将 BERT 的参数减少 40%，并使运行速度提高 71%。DistilBERT 的预训练损失是软蒸馏损失、监督训练损失（即在 BERT 的情况下为 掩码语言模型损失 $\mathcal{L}_\text{MLM}$）和特殊的余弦嵌入损失的组合，以对齐教师和学生之间的隐藏状态向量。

蒸馏可以很容易地与量化 、剪枝 或稀疏化 技术相结合，其中教师模型是原始的全精度、密集模型，而学生模型被量化、剪枝或修剪以具有更高的稀疏度水平。

量化

在深度神经网络上应用量化有两种常见方法：

1. 后训练量化 (PTQ)：首先对模型进行训练至收敛，然后将其权重转换为低精度，无需更多训练。与训练相比，实现起来通常相对便宜。
2. 量化感知训练 (QAT)：在预训练或进一步微调过程中应用量化。QAT 能够获得更好的性能，但需要额外的计算资源和代表性的训练数据。

我们应当意识到理论上最优的量化策略与硬件内核支持之间的差距。由于缺乏某些类型的矩阵乘法（例如 INT4 x FP16）的 GPU 内核支持，下述方法并非所有都能使实际推理速度加快。

Transformer 量化的挑战

许多关于 Transformer 模型量化的研究都有相同的观察：简单的低精度（例如 8 位）后训练量化会导致性能显著下降，主要是由于激活的高动态范围，而一个天真的激活量化策略无法保持容量。

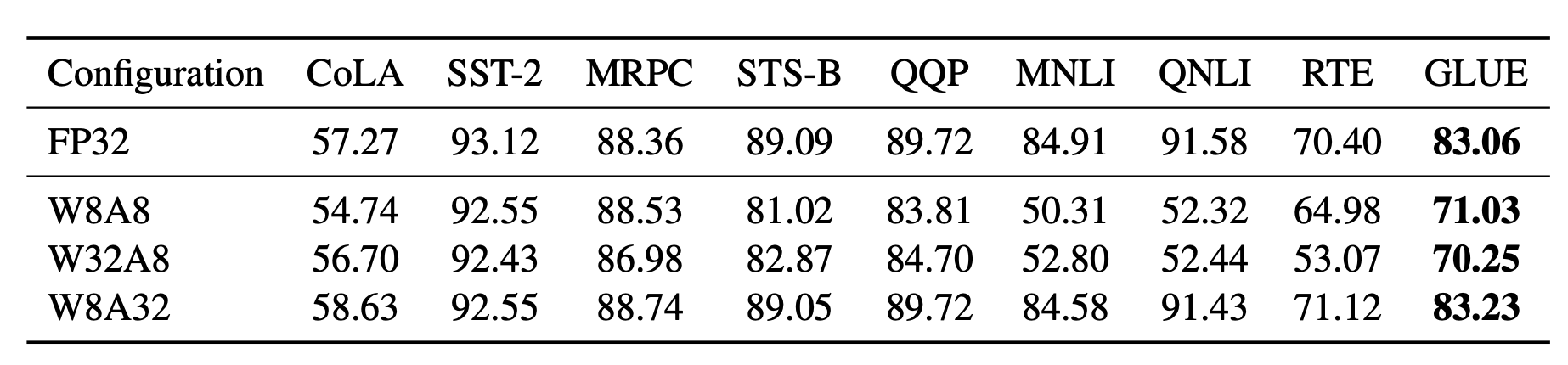
图 2. 只将模型权重量化为 8 位，同时保持激活的全精度（W8A32），比将激活量化为 8 位，无论权重是否为低精度（W8A8 和 W32A8）都能获得更好的结果。 (图片来源：Bondarenko et al. 2021 )

Bondarenko et al. (2021) 在一个小的 BERT 模型中观察到，由于输出张量中的强异常值，FFN 的输入和输出具有非常不同的动态范围。因此，对 FFN 的残差和进行张量量化很可能会导致明显的误差。

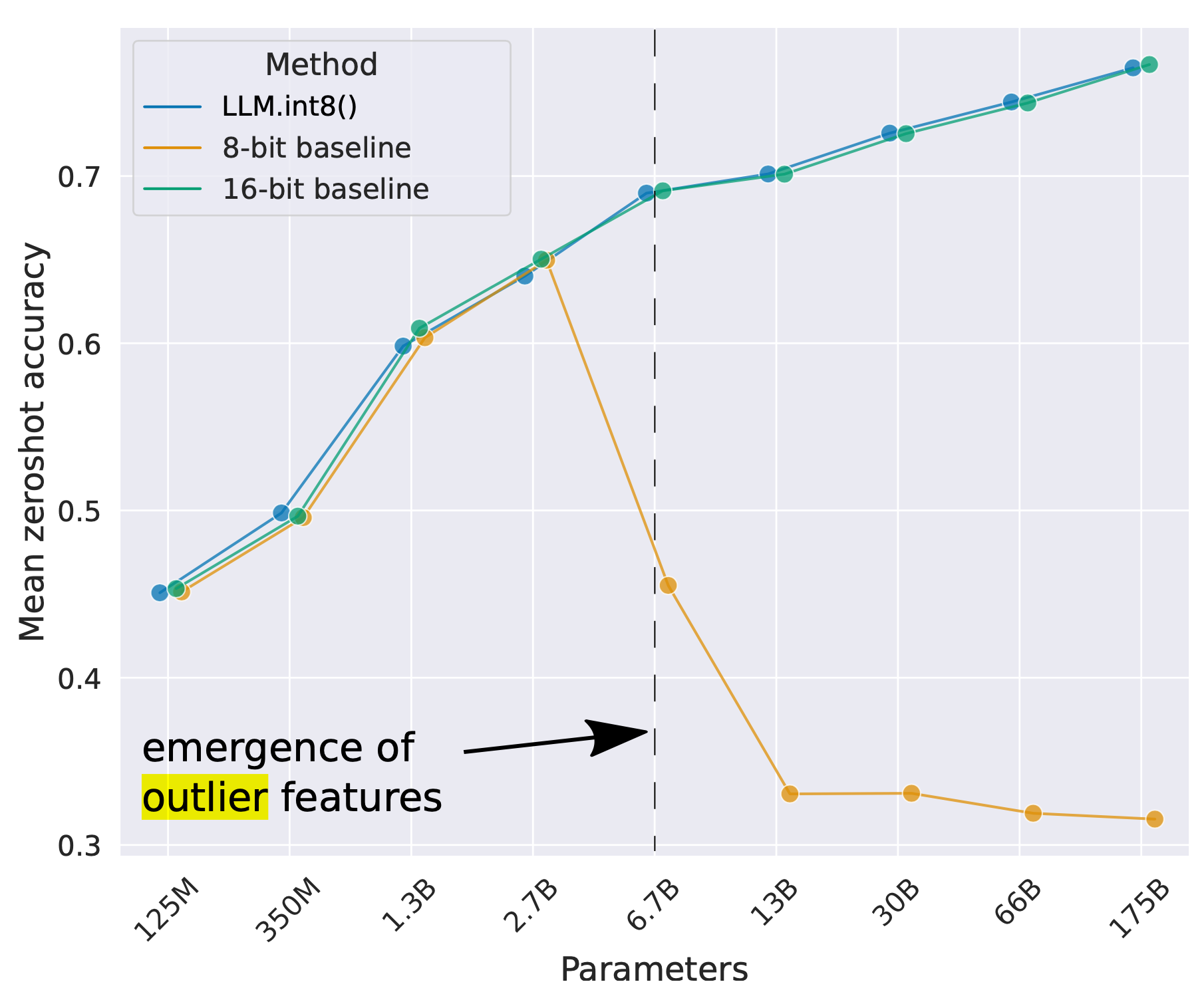
随着模型大小不断增长至数十亿参数，所有 Transformer 层中开始出现高幅度的异常特征，从而导致简单低位量化失败。Dettmers et al. (2022) 观察到 OPT 模型大于 6.7B 参数时出现了这种现象。较大的模型有更多具有极端异常值的层，而这些异常特征对模型性能有显著影响。某些维度中激活异常值的规模可以比大多数其他值大 ~100×。

图 3. 随着 OPT 模型大小的增加，一组语言任务（WinoGrande、HellaSwag、PIQA、LAMBADA）的平均零射击准确率。（图片来源：Dettmers et al. 2022 ）

后训练量化（PTQ）

混合精度量化

解决上述量化挑战的最直接方法是对权重和激活实施不同精度的量化。

GOBO (Zadeh et al. 2020 ) 是首批应用后训练量化（post-training quantization）于 transformer（例如小型的 BERT 模型）的模型之一。它假设每层的模型权重遵循高斯分布，因此通过追踪每层的均值和标准差来检测异常值。异常特征保持原始形式，而其他值则分割成多个箱子（bins），并且只存储权重的相应箱子索引和中心值。

基于只有某些激活层（例如，FFN 后的残差连接）在 BERT 中导致性能大幅下降的观察，Bondarenko et al. (2021) 采用了混合精度量化，对问题激活使用 16 位量化，而对其他激活使用 8 位量化。

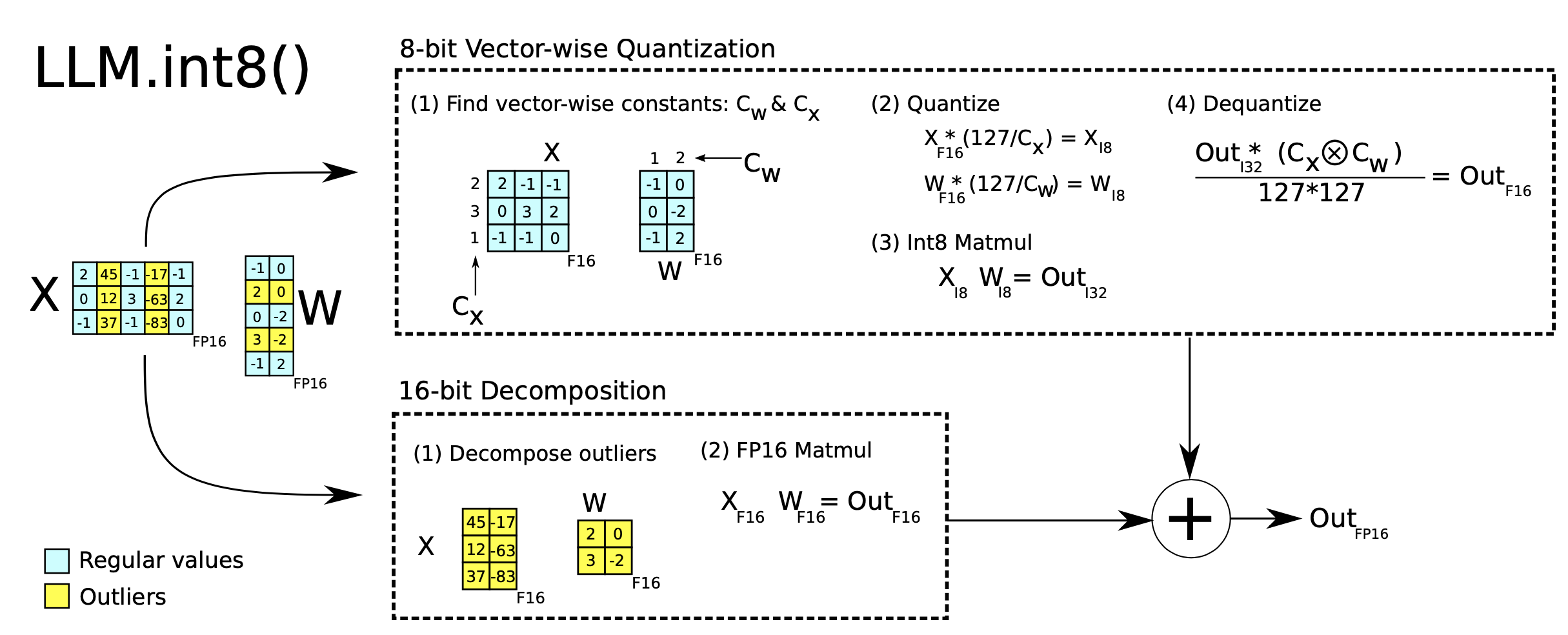
LLM.int8() 中的混合精度量化 (Dettmers et al. 2022 ) 是通过两种混合精度分解来实现的：

1. 由于矩阵乘法包含了行向量和列向量之间一组独立的内积，我们可以对每个内积施加独立的量化：每行和每列按绝对最大值进行缩放，然后量化为 INT8。
2. 异常激活特征（例如，比其他维度大 20 倍）保持在 FP16 中，但它们只占总权重的一小部分。如何识别异常值是基于经验的。

图 4. LLM.int8() 的两种混合精度分解。 (图片来源：Dettmers et al. 2022 )

细粒度量化

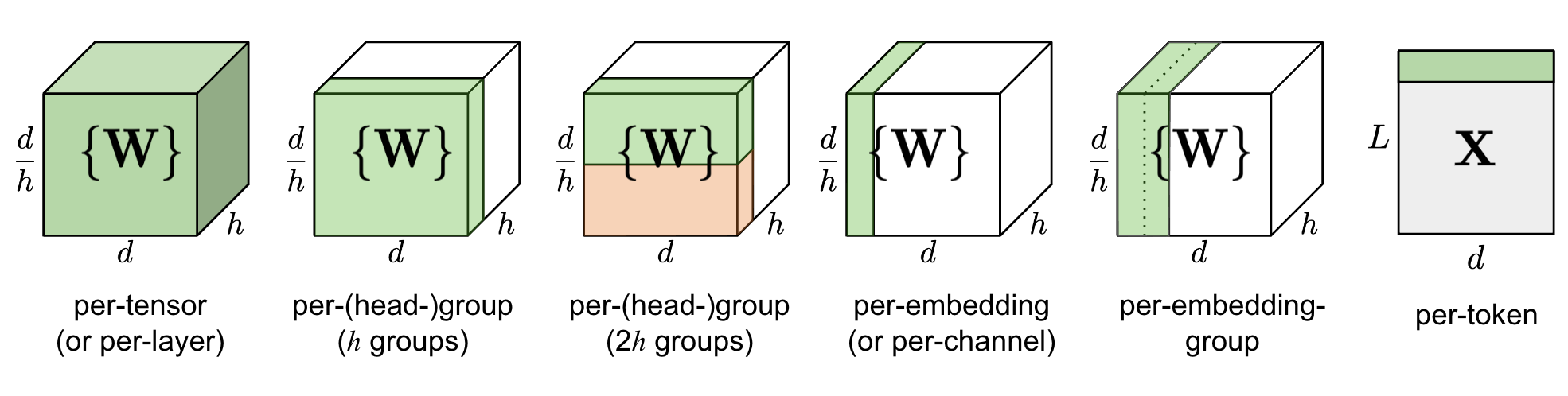
图 5. 不同粒度量化的比较。$d$ 是模型大小/隐藏状态维度，$h$ 是一个 MHSA (多头自注意力) 组件中的头数。

简单地量化一层中的整个权重矩阵（“每张量” 或 “每层” 量化）实现最为简单，但不会导致良好的量化粒度。

Q-BERT (Shen, Dong & Ye, et al. 2020 ) 对微调过的 BERT 模型应用了 组内量化，将 MHSA（多头自注意力）中 每个头 的单独矩阵 $W$ 视为一个组，然后应用基于 Hessian 的混合精度量化。

每嵌入组（PEG） 激活量化是由观察到的异常值只出现在 $d$ （隐藏状态/模型大小）维度中的少数几个维度上所激发的 (Bondarenko et al. 2021 )。每嵌入运算相当耗费计算资源。相比之下，PEG 量化将激活张量沿嵌入维度分割成几个大小相等的组，同一组中的元素共享量化参数。为确保所有异常值被组合在一起，他们应用了基于范围的确定性排列嵌入维度，其中维度按其值范围排序。

ZeroQuant (Yao et al. 2022 ) 对权重使用 组内量化，与 Q-BERT 中的方式相同，对激活使用 逐 Tkoen 量化。为避免昂贵的量化和反量化计算，ZeroQuant 构建了定制的 内核，将量化操作与其前一个操作 融合。

量化的二阶信息

Q-BERT（Shen, Dong & Ye 等人，2020 ）为其混合精度量化开发了 Hessian AWare Quantization（HAWQ）。其动机是具有较高 Hessian 系数（即，较大的顶部特征值）的参数对量化更为敏感，因此需要更高的精度。本质上，这是一种识别异常值的方法。

从另一个角度来看，量化问题是一个优化问题。给定权重矩阵 $ \mathbf{W} $ 和输入矩阵 $ \mathbf{X} $，我们想要找到一个量化的权重矩阵 $ \hat{\mathbf{W}} $ 来最小化 MSE：

$$ \hat{\mathbf{W}}^* = \arg\min_{\hat{\mathbf{W}}} | \mathbf{W}\mathbf{X} - \hat{\mathbf{W}}\mathbf{X}| $$

GPTQ（Frantar 等人，2022 ）将权重矩阵 $ \mathbf{W} $ 视为行向量的集合 $ \mathbf{w} $，并对每行独立应用量化。GPTQ 迭代地量化更多的权重，这些权重是贪婪地选择的，以最小化量化误差。选定的权重更新有一个封闭形式的公式，利用 Hessian 矩阵。如果感兴趣，可以在论文和 OBQ（Optimal Brain Quantization；Frantar & Alistarh 2022 ）方法中阅读更多详情。GPTQ 可以将 OPT-175B 中的权重位宽减少到 3 或 4 位，而不会有太多性能损失，但它只适用于模型权重，而不适用于激活。

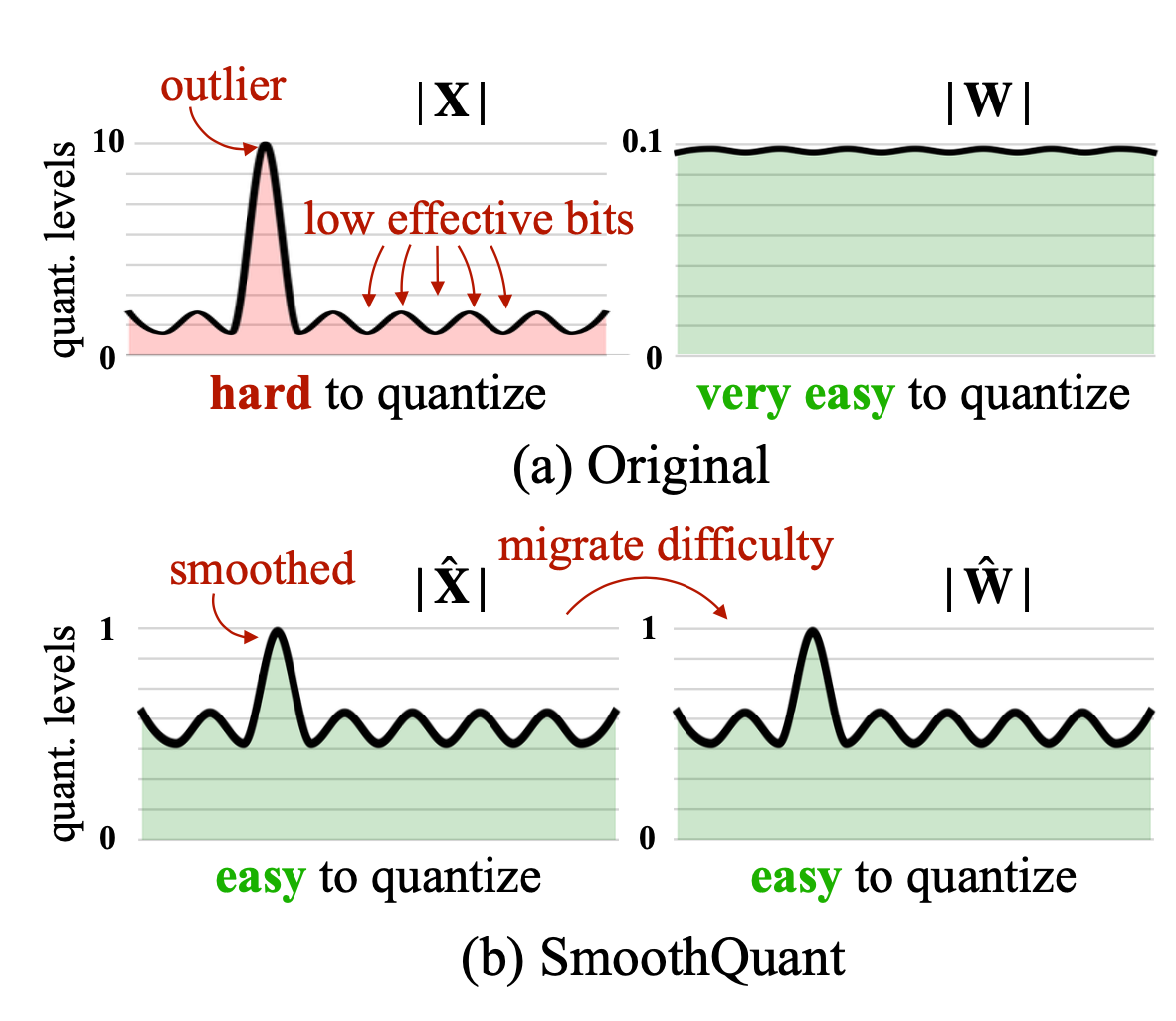
异常值平滑

众所周知，在 transformer 模型中，激活的量化比权重的量化更为困难。SmoothQuant（Xiao & Lin，2022 ）提出了一个聪明的解决方案，通过数学等效变换将异常特征从激活平滑到权重，然后对权重和激活（W8A8）都启用量化。因此，SmoothQuant 具有比混合精度量化更好的硬件效率。

图 6. SmoothQuant 在离线状态下将尺度方差从激活迁移到权重，以减少激活量化的难度。得到的新权重和激活矩阵都易于量化。（图片来源：Xiao & Lin，2022 ）

考虑每通道平滑因子 $ \mathbf{s} $，SmoothQuant 按照以下方式缩放权重：

$ \mathbf{Y} = (\mathbf{X} \text{diag}(\mathbf{s})^{-1}) \cdot (\text{diag}(\mathbf{s})\mathbf{W}) = \hat{\mathbf{X}}\hat{\mathbf{W}} $

平滑因子可以很容易地融入离线的先前层的参数中。超参数 $ \alpha $ 控制我们将量化难度从激活迁移到权重的程度：$ \mathbf{s} = \max (| \mathbf{X}_j |)^\alpha / \max( | \mathbf{W}_j |)^{1-\alpha} $。论文发现，对于许多实验中的 LLM，$ \alpha=0.5 $ 是一个甜蜜点。对于激活中具有更显著异常值的模型，可以调整 $ \alpha $ 以使其更大。

量化感知训练（QAT）

量化感知训练将量化操作融入到预训练或精调过程中。它直接以低位表示形式学习模型权重，并以额外的训练时间和计算为代价，带来了更好的性能。

最直接的方法是在量化后对模型进行精调，使用与预训练数据集相同或具有代表性的训练数据集。训练目标可以与预训练相同（例如，通用语言模型训练中的 NLL/MLM）或特定于我们关心的下游任务（例如，分类的交叉熵）。

另一种方法是将全精度模型视为教师模型，将低精度模型视为学生模型，然后使用蒸馏损失优化低精度模型。蒸馏通常不需要使用原始数据集；例如，Wikipedia 数据集是一个不错的选择，甚至随机 Tkoen 也可以带来不错的性能提升。逐层知识蒸馏（LKD；Yao 等，2022 ）方法逐层量化网络，并使用其原始的、未量化的版本作为教师模型。在给定相同输入的情况下，LKD 最小化了层权重乘法和量化层权重乘法之间的 MSE。

剪枝

网络剪枝旨在通过修剪不重要的模型权重或连接来减小模型大小，同时保持模型容量。它可能需要或可能不需要重新训练。剪枝可以是非结构化的或结构化的。

• 非结构化剪枝允许丢弃任何权重或连接，因此它不保留原始网络架构。非结构化剪枝通常不适用于现代硬件，并且不会导致实际推理速度的提升。
• 结构化剪枝旨在保持密集矩阵乘法形式，其中某些元素为零。他们可能需要遵循某些模式限制以适应硬件内核支持。在这里，我们关注结构化剪枝以实现 Transformer 模型中的高稀疏性。

构建剪枝网络的常规工作流程 包括三个步骤：

1. 训练密集网络直至收敛；
2. 剪枝网络以移除不需要的结构；
3. 可选地重新训练网络以使用新权重恢复性能。

通过网络剪枝在密集模型中发现稀疏结构的想法，同时稀疏网络仍然可以保持相似的性能，是受彩票票据假设 （LTH）的启发：一个随机初始化的、密集的、前馈网络包含一个子网络池，其中只有一个子集（一个稀疏网络）是*“中奖票”*，当它们单独训练时可以实现最优性能。

如何剪枝？

幅度剪枝 是最简单但相当有效的剪枝方法 —— 会修剪绝对值最小的权重。实际上，一些研究（Gale et al. 2019 ）发现 简单的幅度剪枝方法可以获得与复杂剪枝方法相当或更好的结果，例如变分丢弃 （Molchanov et al. 2017 ）和 $ l_0 $ 正则化（Louizos et al. 2017 ）。幅度剪枝易于应用于大型模型，并在多种超参数范围内取得了相当稳定的性能。

Zhu & Gupta (2017) 发现 大型稀疏模型能够比其小型但密集的对应物取得更好的性能。他们提出了 逐渐幅度剪枝 (GMP) 算法，该算法逐渐增加网络的稀疏度。在每个训练步骤中，绝对值最小的权重被屏蔽为零，以实现所需的稀疏度水平 $ s $，并且在反向传播过程中，屏蔽的权重不会得到梯度更新。随着训练步骤的增加，所需的稀疏度水平 $ s $ 会增加。GMP 的过程对学习率计划敏感，该计划应高于密集网络训练中使用的学习率，但不能太高以防止收敛。

迭代剪枝 (Renda et al. 2020 ) 多次重复步骤 2（剪枝）和步骤 3（重新训练）：每次迭代只剪枝一小部分权重，并对模型进行重新训练。该过程重复，直到达到所需的稀疏度水平。

如何重新训练？

重新训练步骤可以是使用相同的预训练数据或其他特定任务数据集进行简单的微调。

彩票假说 提出了一种 权重回溯 重新训练技术：剪枝后，未剪枝的权重重新初始化为训练早期的原始值，然后按照相同的学习率计划进行重新训练。

学习率回溯 (Renda et al. 2020 ) 只将学习率重置为早期值，而未剪枝的权重自上次训练阶段结束以来保持不变。他们观察到（1）在所有测试场景中，权重回溯的重新训练优于微调的重新训练，以及（2）学习率回溯在所有测试场景中均匹配或优于权重回溯。

稀疏性

稀疏性是在保持模型推理计算效率的同时扩展模型容量的有效方式。在这里，我们考虑了转换器的两种稀疏性类型：

• 稀疏化密集层，包括自注意力和 FFN 层。
• 稀疏模型架构；即通过整合 Mixture-of-Experts (MoE) 组件。

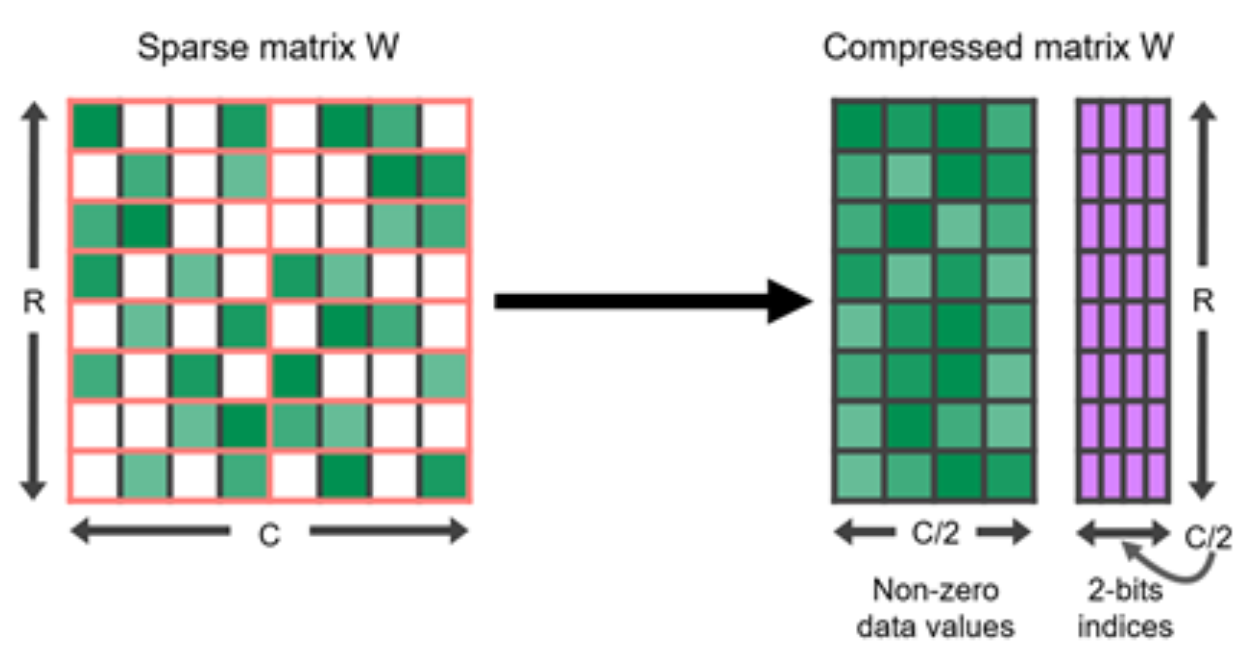
通过剪枝实现的 N:M 稀疏性

N:M 稀疏性 是一种与现代 GPU 硬件优化良好协作的结构化稀疏模式，在这种模式中，每 $M$ 个连续元素中的 $N$ 个元素是零。例如，Nvidia A100 GPU 的稀疏张量核心支持 2:4 稀疏性以实现更快的推理（Nvidia 2020 ）。

图 7. 2:4 结构化稀疏矩阵及其压缩表示。 (图片来源：Nvidia blog )

为了使密集神经网络遵循 N:M 结构化稀疏模式，Nvidia (2020) 建议使用三步常规工作流 来训练剪枝网络：训练 –> 剪枝以满足 2:4 稀疏性 –> 重新训练。

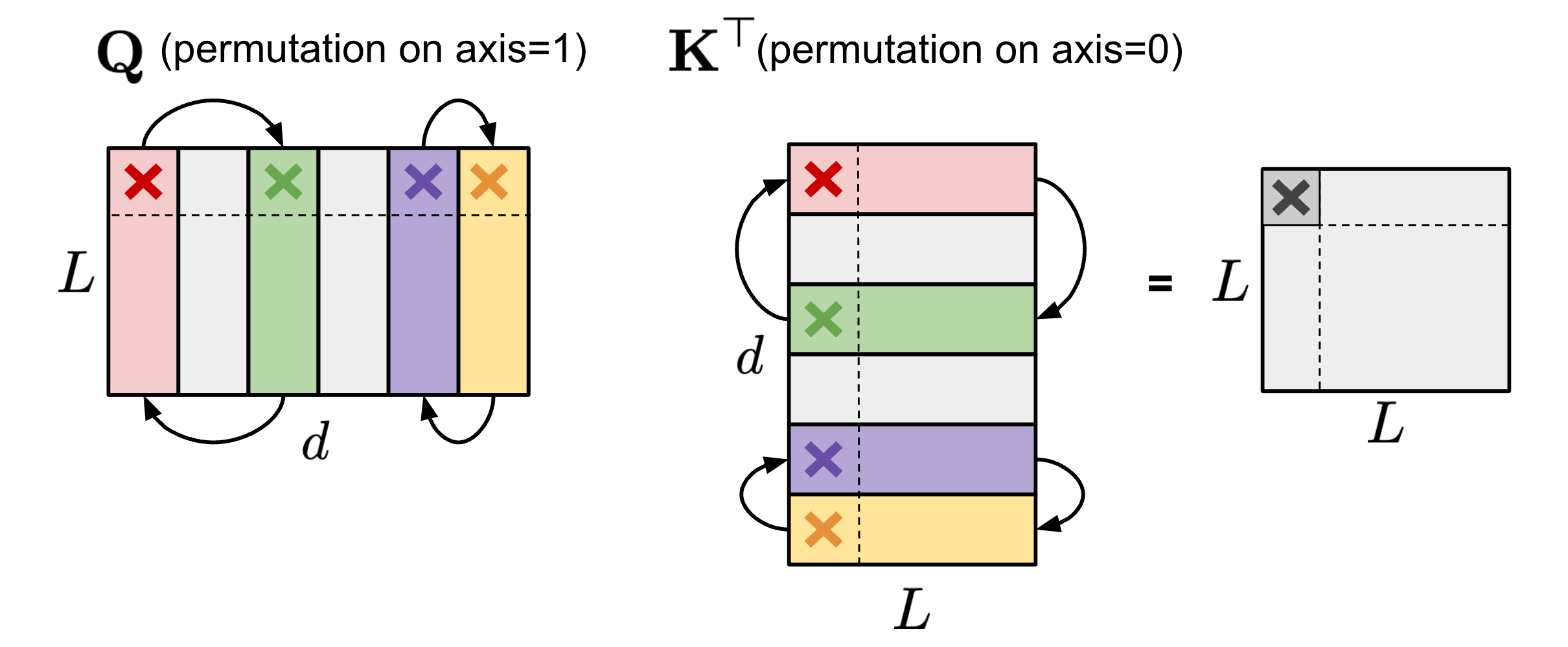
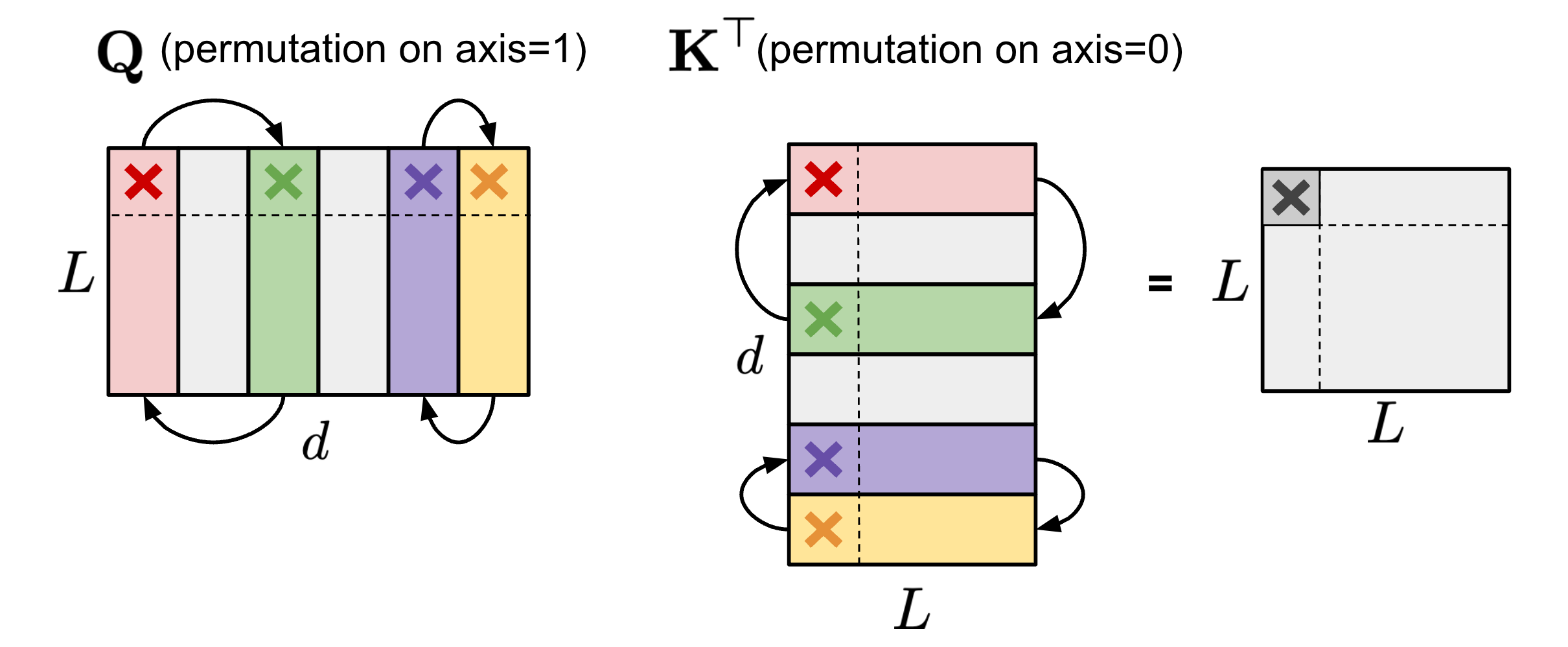
排列列可以在剪枝过程中提供更多选项，以保留大幅度的参数或满足特殊的限制，如 N:M 稀疏性（Pool & Yu 2021 ）。只要两个矩阵的配对轴以相同的顺序排列，矩阵乘法的结果就不会改变。例如，

$ 1 $ 在自注意力模块中，如果在查询嵌入矩阵 $\mathbf{Q}$ 的轴 1 和键嵌入矩阵 $\mathbf{K}^\top$ 的轴 0 上应用相同的排列顺序，那么 $\mathbf{Q}\mathbf{K}^\top$ 的矩阵乘法的最终结果将保持不变。

图 8. 保持自注意力模块结果不变的 $\mathbf{Q}$（轴 1）和 $\mathbf{K}^\top$（轴 0）的相同排列示意图。

$ 2 $ 在包含两个 MLP 层和一个 ReLU 非线性层的 FFN 层中，我们可以按相同的顺序排列第一个线性权重矩阵 $\mathbf{W}_1$（沿着轴 1）和第二个线性权重矩阵 $\mathbf{W}_2$（沿着轴 0）。

图 9. 保持 FFN 层输出不变的 $\mathbf{W}_1$（轴 1）和 $\mathbf{W}_2$（轴 0）的相同排列示意图。为简单起见，省略了偏置项，但应在它们上也应用相同的排列。

为了执行 N:M 结构化稀疏，让我们将一个矩阵的列分成多个包含 $M$ 列的片段（名为 “stripe”），我们可以轻松地观察到，每个条纹内的列的顺序和条纹的顺序对 N:M 稀疏限制没有影响。

Pool & Yu (2021) 提出了一种迭代贪婪算法，以找到最大化 N:M 稀疏性的权重幅度的最优排列。所有通道对都被推测性地交换，只有导致幅度最大增加的交换被采纳，从而生成新的排列并结束单次迭代。贪婪算法可能只会找到局部最小值，因此他们引入了两种技术来逃脱局部最小值：

1. 有界回归：在实践中，两个随机通道被交换，最多交换固定次数。解决方案搜索仅限于一个通道交换的深度，以保持搜索空间宽而浅。
2. 狭窄、深度搜索：选择多个条纹并同时优化它们。

图 10. 寻找 N:M 稀疏性的最佳排列的算法，贪婪且迭代地进行。（图片来源：Pool & Yu 2021 ）

如果网络在修剪之前进行排列，与在默认通道顺序中修剪网络相比，它可以获得更好的性能。

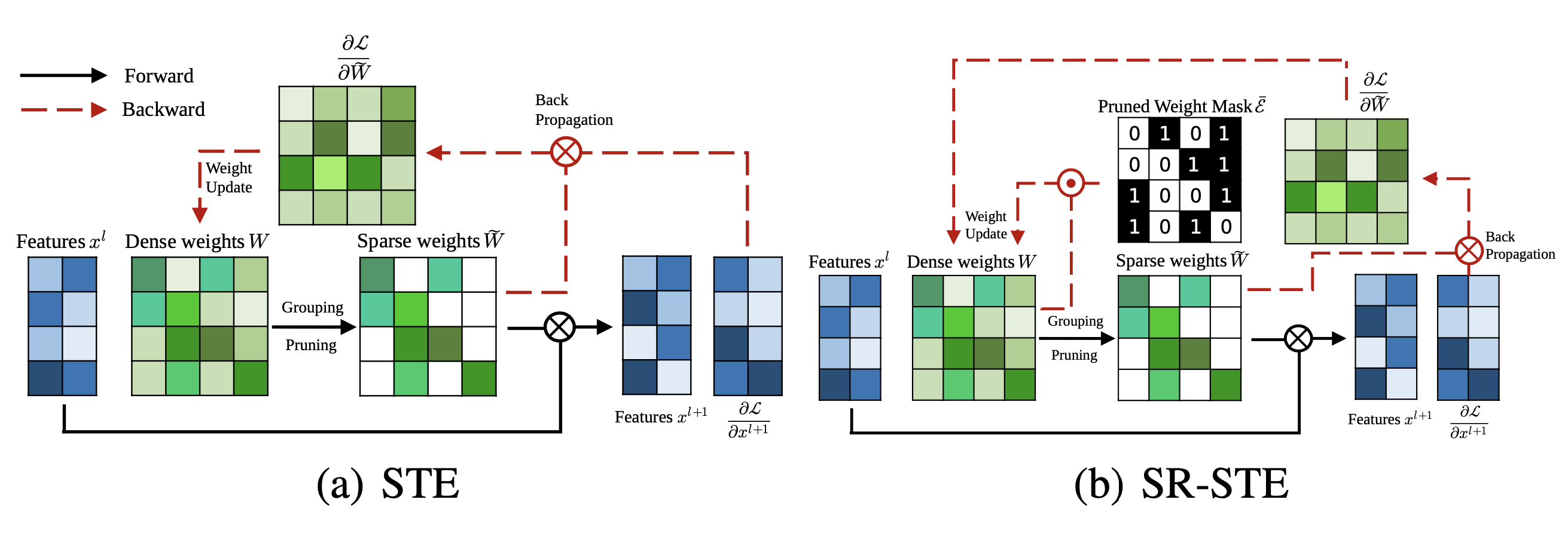
为了从头开始训练具有 N:M 稀疏性的模型，Zhou & Ma, 等人 2021 扩展了 STE (Straight-Through Estimator；Bengio 等人 2013 )，它通常用于模型量化中的反向传播更新，以便用于幅度修剪和稀疏参数更新。

STE 计算相对于修剪网络 $ \widetilde{W} $ 的稠密参数的梯度 $ \partial \mathcal{L}/\partial \widetilde{W} $，并将其作为近似应用于稠密网络 $ W $：

$$ W_{t+1} \gets W_t - \gamma \frac{\partial\mathcal{L}}{\partial\widetilde{W}} $$

扩展版本，SR-STE (Sparse-refined STE)，通过以下方式更新稠密权重 $W$：

$$ W_{t+1} \gets W_t - \gamma \frac{\partial\mathcal{L}}{\partial\widetilde{W}} + \lambda_W (\bar{\mathcal{E}} \odot W_t) $$

其中 $\bar{\mathcal{E}}$ 是 $\widetilde{W}$ 的掩码矩阵，$\odot$ 是元素对应乘法。SR-STE 旨在通过（1）限制在 $\widetilde{W}_t$ 中修剪的权重值，并且（2）提升 $\widetilde{W}_t$ 中未修剪的权重，以防止二进制掩码发生较大变化。

图 11. STE 和 SR-STE 的比较。$\odot$ 是元素对应乘法；$\otimes$ 是矩阵乘法。（图片来源：Zhou & Ma, 等人 2021 ）

与 STE 或 SR-STE 不同，Top-KAST（Jayakumar 等人 2021 ）方法可以在训练的前向和反向传播中保持恒定的稀疏性，但不需要具有稠密参数或稠密梯度的前向传播。

在一个训练步骤 $ t $ 中，Top-KAST 进程如下：

1. 稀疏前向传播：选择参数子集 $ A^t \subset \Theta $，其中每层的参数子集包含按幅度排列的前-$ K $ 参数，限制为前 $ D $-比例的权重。在时间 $ t $ 时，如果不在 $ A^t $ 中（活动权重），参数化 $ \alpha^t $ 的参数将被清零。

$$ \alpha^t_i = \begin{cases} \theta^t_i & \text{ if } i \in A^t = {i \mid \theta^t_i \in \text{TopK}(\theta^t, D) }\\ 0 & \text{ otherwise} \end{cases} $$

其中 $ \text{TopK}(\theta, x) $ 根据幅度从 $ \theta $ 中选择前 $ x $ 比例的权重。

2. 稀疏反向传播：然后将梯度应用于较大的参数子集 $ B \subset \Theta $，其中 $ B $ 包含 $ (D+M) $-比例的权重，且 $ A \subset B $。更新较大比例的权重可以更有效地探索不同的修剪掩码，使得更可能在前 $ D $-比例的活动权重中引起排列。

   $$ \Delta_{\theta^t_i} = \begin{cases} -\eta \nabla_{\alpha_t} \mathcal{L}(y, x, \alpha^t)_i & \text{ if } i\in B^t = {i \mid \theta^t_i \in \text{TopK}(\theta^t, D+M) } \\ 0 & \text{ otherwise } \end{cases} $$

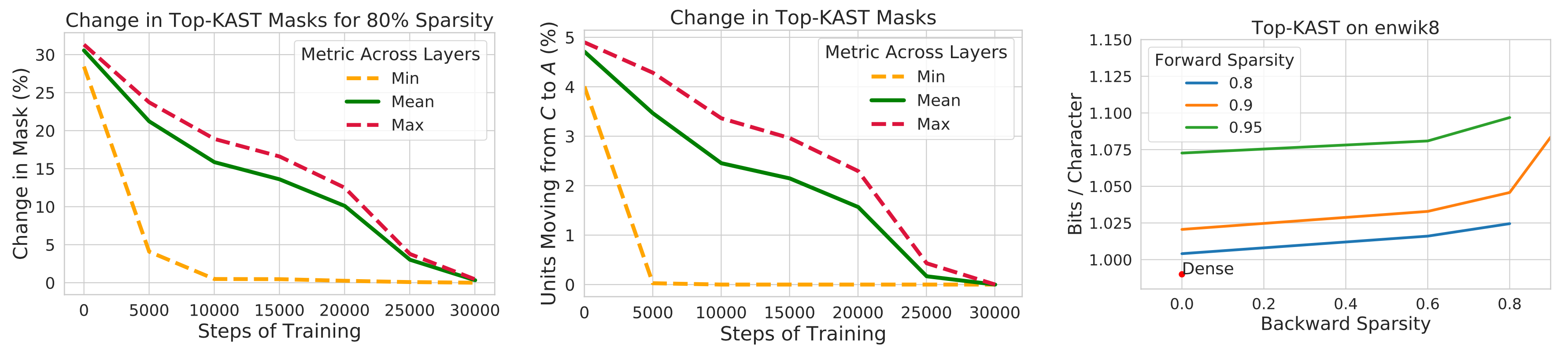
训练分为两个阶段，集合 $B \setminus A$ 中的额外坐标控制引入了多少探索。探索的数量预计会在训练过程中逐渐减少，掩码最终会稳定。

图 12. Top-KAST的剪枝掩码随时间稳定。(图片来源：Jayakumar等人，2021 )

为了防止富者愈富现象，Top-KAST通过L2正则化损失来惩罚活动权重的幅度，以鼓励对新项目的更多探索。在$B \setminus A$中的参数比在$A$中的参数受到更多的惩罚，以在更新时提高选择标准，稳定掩码。

稀疏化 Transformer

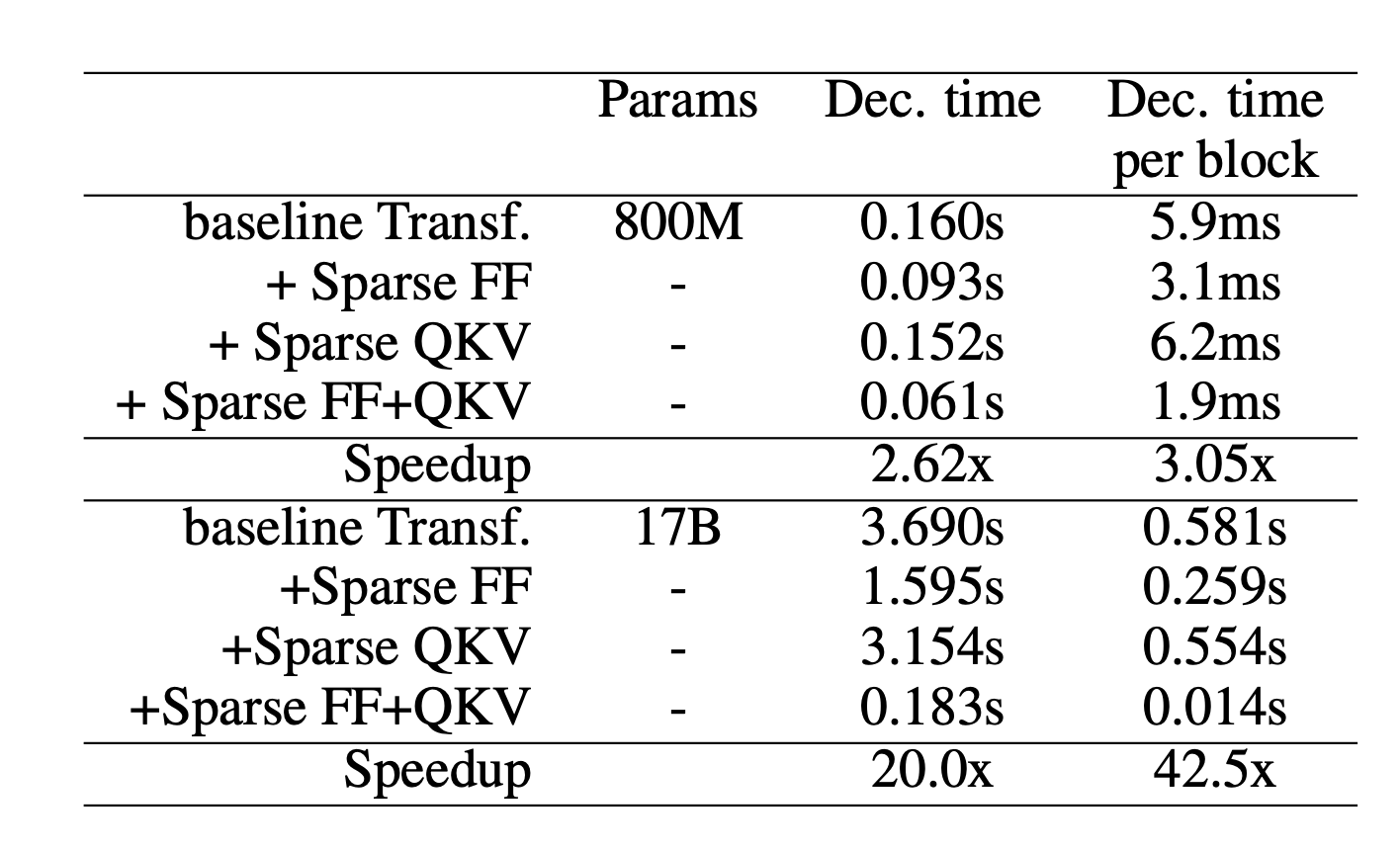
Scaling Transformer（Jaszczur等人，2021 ）在 transformer 架构中稀疏化了自注意力和 FFN 层，实现了对单个样例推理的 37 倍加速。

图 13. 在不同层应用稀疏化时，transformer 模型解码单个 Tkoen （未分批推理）的速度。（图片来源：Jaszczur等人，2021 ）

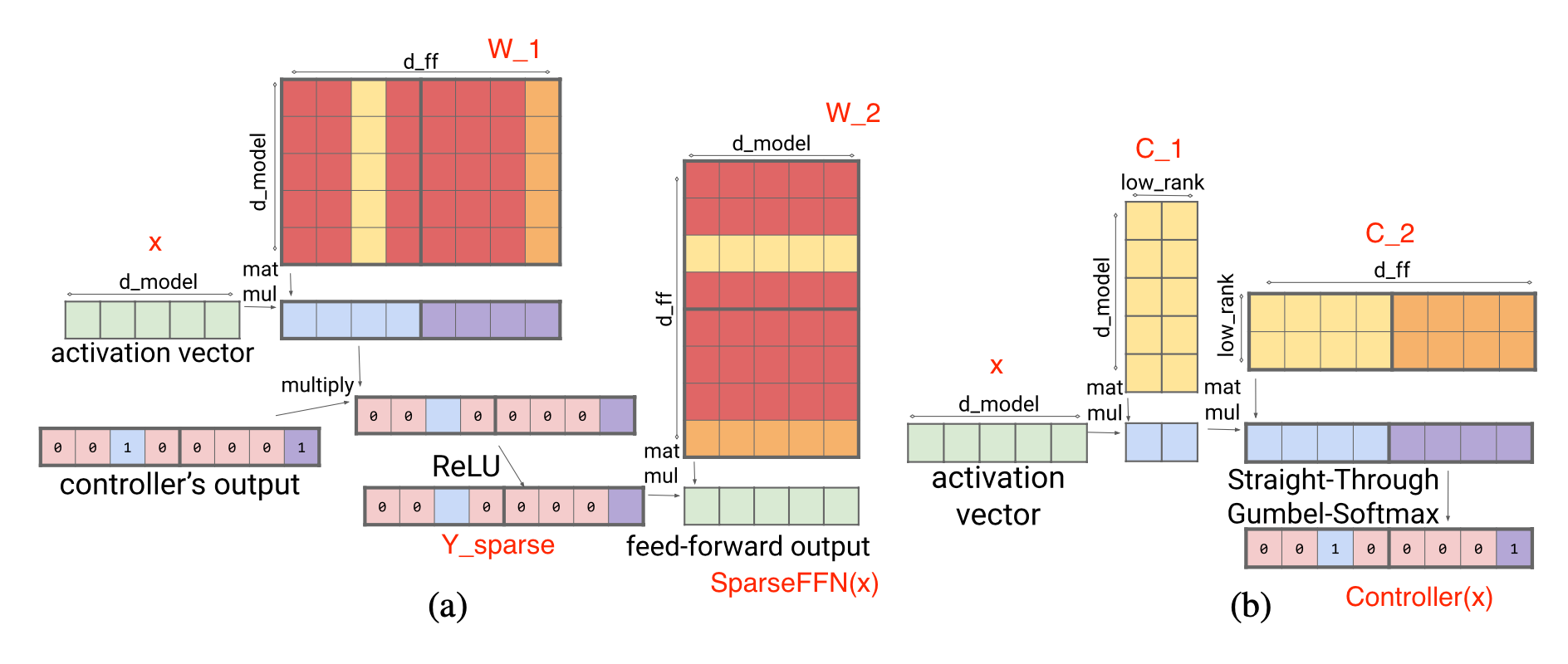
稀疏 FFN 层：每个 FFN 层包含 2 个 MLP 和一个 ReLU，在两者之间。由于 ReLU 会引入许多零，他们在激活上实现了固定结构，以在一个由 $N$ 个元素组成的块中仅强制一个非零值。稀疏模式是动态的，每个 Tkoen 都不同。

其中 $Y_\text{sparse}$ 中的每个激活对应于 $W_1$ 中的一列和 $W_2$ 中的一行。控制器被实现为低秩瓶颈密集层，$C_1 \in \mathbb{R}^{d_\text{model} \times d_\text{lowrank}}, C_2 \in \mathbb{R}^{d_\text{lowrank} \times d_\text{ff}}$，且 $d_\text{lowrank} = d_\text{model} / N$。它在推理时使用 $\arg\max$ 来选择哪些列应该为非零，并在训练期间使用 Gumbel-softmax 技巧（Jang等人，2016 ）。由于我们可以在加载 FFN 权重矩阵之前计算 $\text{Controller}(x)$，我们知道哪些列将被清零，因此选择 不加载 它们以加速推理。

图 14. (a) 稀疏 FFN 层；红色列没有加载到内存中，以便更快地推理。 (b) 1:4 稀疏度的稀疏 FFN 控制器。（图片来源：Jaszczur等人，2021 ） Lilian的附注：论文中的图 (a) 描述实际上是 $Y_\text{sparse} = \max\big(0, (xW_1 + b_1) \odot \text{Controller}(x)\big)$，但这不会改变结果。

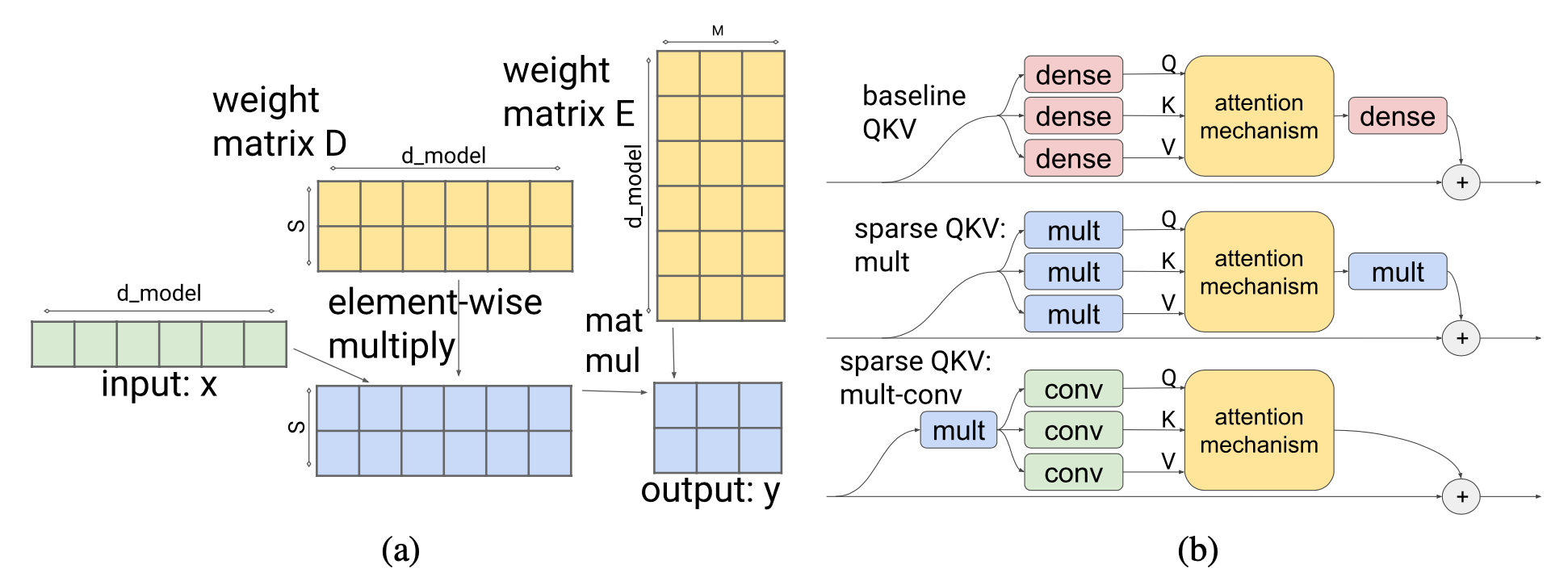
稀疏 QKV（注意力）层：在注意力层中，维数 $d_\text{model}$ 被划分为 $S$ 个模块，每个模块的大小为 $M=d_\text{model} /S$。为了确保每个细分都能访问嵌入的任何部分，Scaling Transformer 引入了一个乘法层（即，乘法层按元素方式乘以来自多个神经网络层的输入），它可以表示任意排列，但参数少于密集层。

对于输入向量 $x \in \mathbb{R}^{d_\text{model}}$，乘法层输出 $y \in \mathbb{R}^{S \times M}$：

乘法层的输出是一个大小为 $\in \mathbb{R}^{\text{batch size}\times \text{length} \times S \times M}$ 的张量。然后它通过一个二维卷积层进行处理，其中 $\text{length}$ 和 $S$ 被视为图像的高度和宽度。这样的卷积层进一步减少了注意力层的参数数量和计算时间。

图 15. (a) 引入了一个乘法层，以使分区能够访问嵌入的任何部分。 (b) 乘法密集层和 2-D 卷积层的组合减少了注意力层的参数数量和计算时间。（图片来源：Jaszczur 等，2021 ）

为了更好地处理长序列，Scaling Transformer 进一步配备了来自 Reformer 的 LSH（局部敏感哈希）注意力 (Kitaev, et al. 2020 ) 和 FFN 块递归，从而产生了 Terraformer。

Mixture-of-Experts

Mixture-of-experts（MoE）模型依赖于一组“专家”网络，每个示例只激活网络的一个子集以获得预测。该想法可以追溯到 1990 年代 (Jacobs et al. 1991 )，与集成方法有很强的关联。有关如何将 MoE 模块整合到 transformer 中的详细信息，请查看我之前关于大型模型训练技术的 博文 和 MoE 的调查论文 Fedus et al. 2022 。

借助 MoE 架构，在解码时只使用部分参数，从而节省了推理成本。每个专家的容量可以通过超参数，容量因子 $C$，进行调整，专家容量定义为：

其中每个 Tkoen 选择 top-$k$ 专家。较大的 $C$ 导致更高的专家容量和改善的性能，但计算成本更高。当 $C>1$ 时，会添加一个松散容量；否则，当 $C<1$ 时，路由网络需要忽略一些 Tkoen 。

路由策略改进

MoE 层具有一个路由网络，为每个输入 Tkoen 分配一组专家的子集。在原始的 MoE 模型中，路由策略是按照它们在自然顺序中出现的顺序，将每个 Tkoen 路由到不同的首选专家。如果一个 Tkoen 被路由到已达到其容量的专家，则该 Tkoen 将被标记为 “溢出”并跳过。

V-MoE（Vision MoE；Riquelme et al. 2021 ）将 MoE 层添加到 ViT（Vision Transformer）。它与先前的 SoTA 性能相匹配，但仅需要 一半 的推理计算。V-MoE 可以扩展到 150 亿参数。他们的实验使用 $k=2$，32 个专家和 every-2 专家布置（意味着 MoEs 每隔一层放置）。

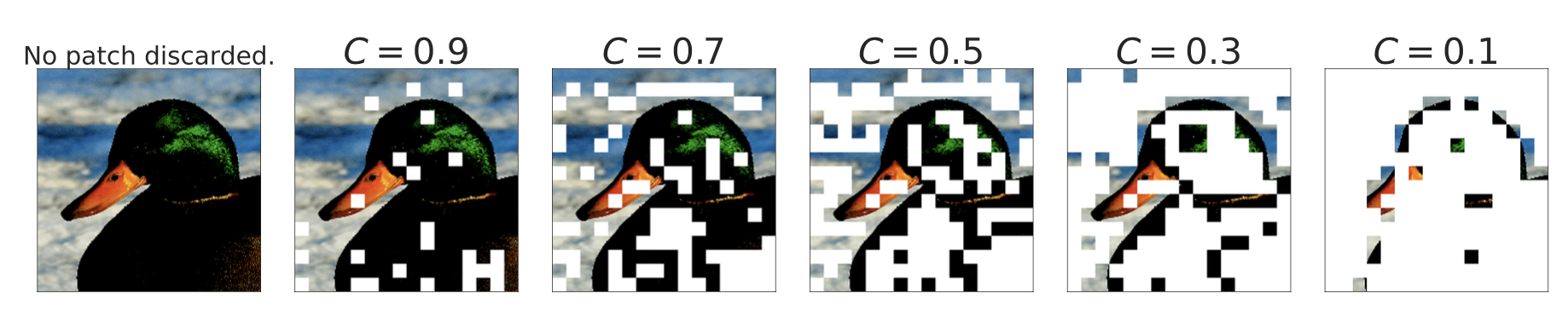
由于每个专家的容量有限，如果它们在预定义的序列顺序中出现太晚（例如，句子中的单词顺序或图像补丁的顺序），一些重要且信息丰富的 Tkoen 可能必须被丢弃。为了避免原始路由方案中的这种缺点，V-MoE 采用 BPR（Batch Priority Routing，批量优先路由） 首先为具有高优先级得分的 Tkoen 分配专家。BPR 在专家分配之前为每个 Tkoen 计算优先级得分（最大值或 top-$k$ 路由器得分的总和），并相应地改变 Tkoen 的顺序。这确保了专家容量缓冲区首先会用关键 Tkoen 填充。

图 16. 如何根据优先级分数丢弃图像块当 $C < 1$ 时（图片来源：Riquelme 等人 2021 ）

BPR 在 $C \leq 0.5$ 时的表现比普通的路由要好得多，在这个点模型开始丢弃大量的令牌。它使模型即使在相当低的容量下也能与密集网络竞争。

在探究如何解释图像类-专家关联时，他们观察到早期的 MoE 层更为通用，而后期的 MoE 层可能会针对少数图像类别而专门化。

任务 MoE （Task-level Mixture-of-Experts；Kudugunta 等人 2021 ）将任务信息考虑在内，并在 任务 级别而不是单词或令牌级别上对令牌进行路由，以进行机器翻译。他们以 MNMT（多语言神经机器翻译）为例，并根据目标语言或语言对对翻译任务进行分组。

令牌级别的路由是动态的，每个令牌的路由决策是分离的。因此，在推理时，服务器需要预加载所有的专家。相比之下，任务级路由在给定固定任务时是 静态 的，因此一个任务的推理服务器只需要预加载 $k$ 个专家（假设采用 top-$k$ 路由）。根据他们的实验，与密集模型基线相比，任务 MoE 可以实现类似的性能增益，具有 2.6 倍的最高吞吐量和解码器大小的 1.6%。

任务级 MoE 的本质是根据预定义的 启发式方法 对任务分布进行分类，并将这种人类知识融入到路由器中。当这种启发式方法不存在时（例如，考虑一项通用的句子延续任务），使用任务 MoE 的方法并不明确。

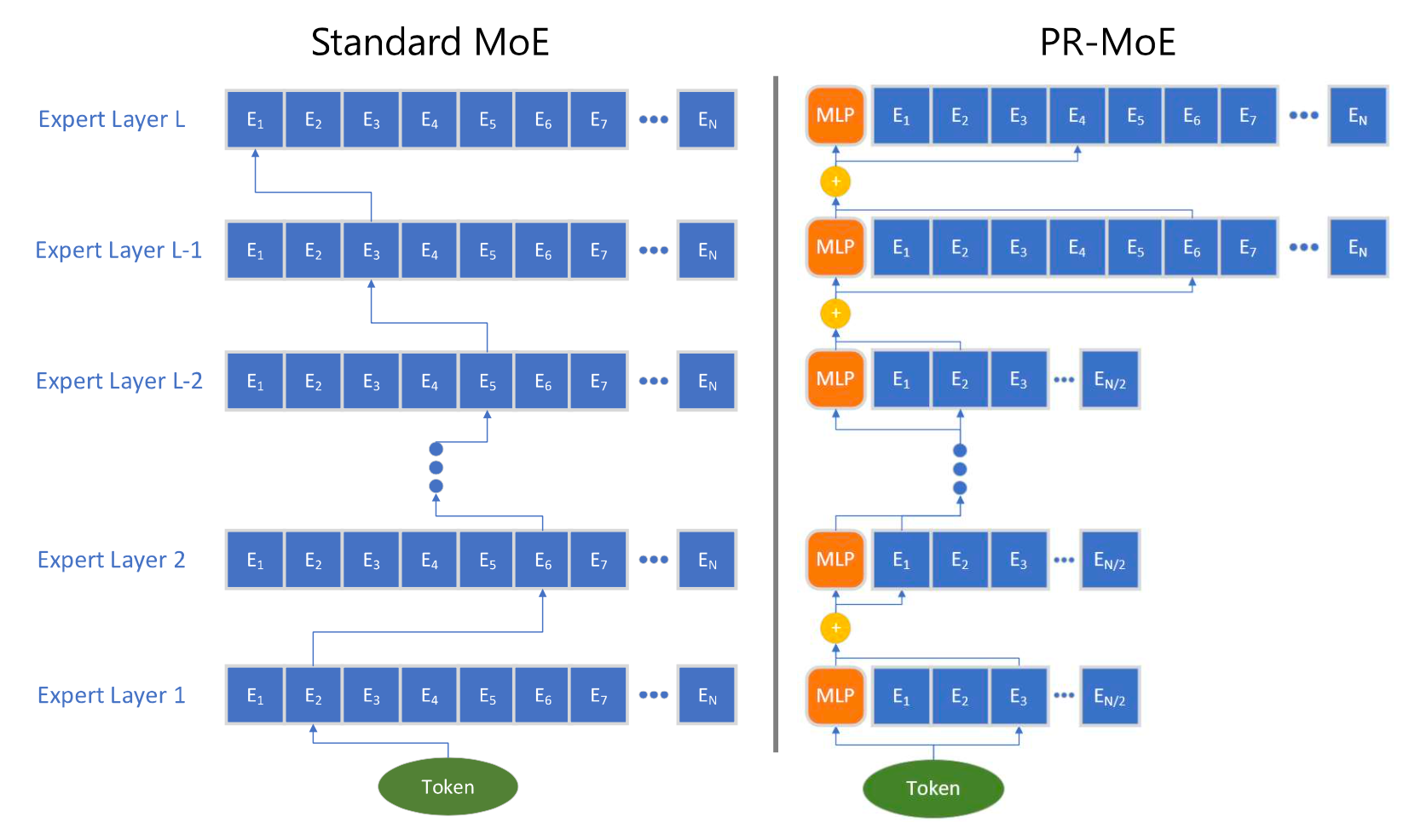
PR-MoE （Pyramid residual MoE；Rajbhandari 等人 2022 ）使每个令牌通过一个固定的 MLP 和一个选定的专家。由于观察到在后期层的 MoE 更为有益，PR-MoE 在后期层采用了更多的专家。DeepSpeed 库实现了灵活的多专家、多数据并行性，以便使用不同数量的专家跨层训练 PR-MoE。

图 17. 与标准 MoE 相比，PR-MoE 架构的示意图（图片来源：Rajbhandari 等人 2022 ）

内核改进

专家网络可以托管在不同的设备上。但是，当 GPU 的数量增加时，每个 GPU 的专家数量减少，而专家之间的通信（“全对全”）变得更为昂贵。大量 GPU 之间的专家“全对全”通信依赖于 NCCL 的 P2P API，但在大规模时无法饱和高速链接（例如 NVLink，HDR InfiniBand）的带宽，因为随着更多节点的使用，单个块变得更小。现有的全对全算法在大规模、小工作负载下表现不佳。有多种内核改进可以实现更高效的 MoE 计算，例如使全对全通信更便宜/更快。

DeepSpeed 库（Rajbhandari 等人 2022 ）和 TUTEL（Hwang 等人 2022 ）实现了基于树的分层全对全算法，该算法首先运行节点内全对全，然后运行节点间全对全。它将通信跳数从 $O(G)$ 减少到 $O(G_\text{node} + G / G_\text{node})$，其中 $G$ 是 GPU 节点的总数，$G_\text{node}$ 是每个节点的 GPU 核心数。尽管此类实现中的通信量加倍，但它在小批量的大规模时实现了更好的缩放，因为在批量大小小时，瓶颈在延迟而不是通信带宽上。

DynaMoE （Kossmann 等人 2022 ）使用动态重新编译来适应专家之间的动态工作负载。RECOMPILE 机制从头开始编译计算图，并仅在需要时重新分配资源。它衡量了分配给每个专家的样本数量，并动态调整其容量因子 $C$，以减少运行时的内存和计算需求。基于观察到样本-专家分配在训练早期收敛的情况，引入了样本分配缓存，然后使用 RECOMPILE 来消除门控网络和专家之间的依赖性。

架构优化

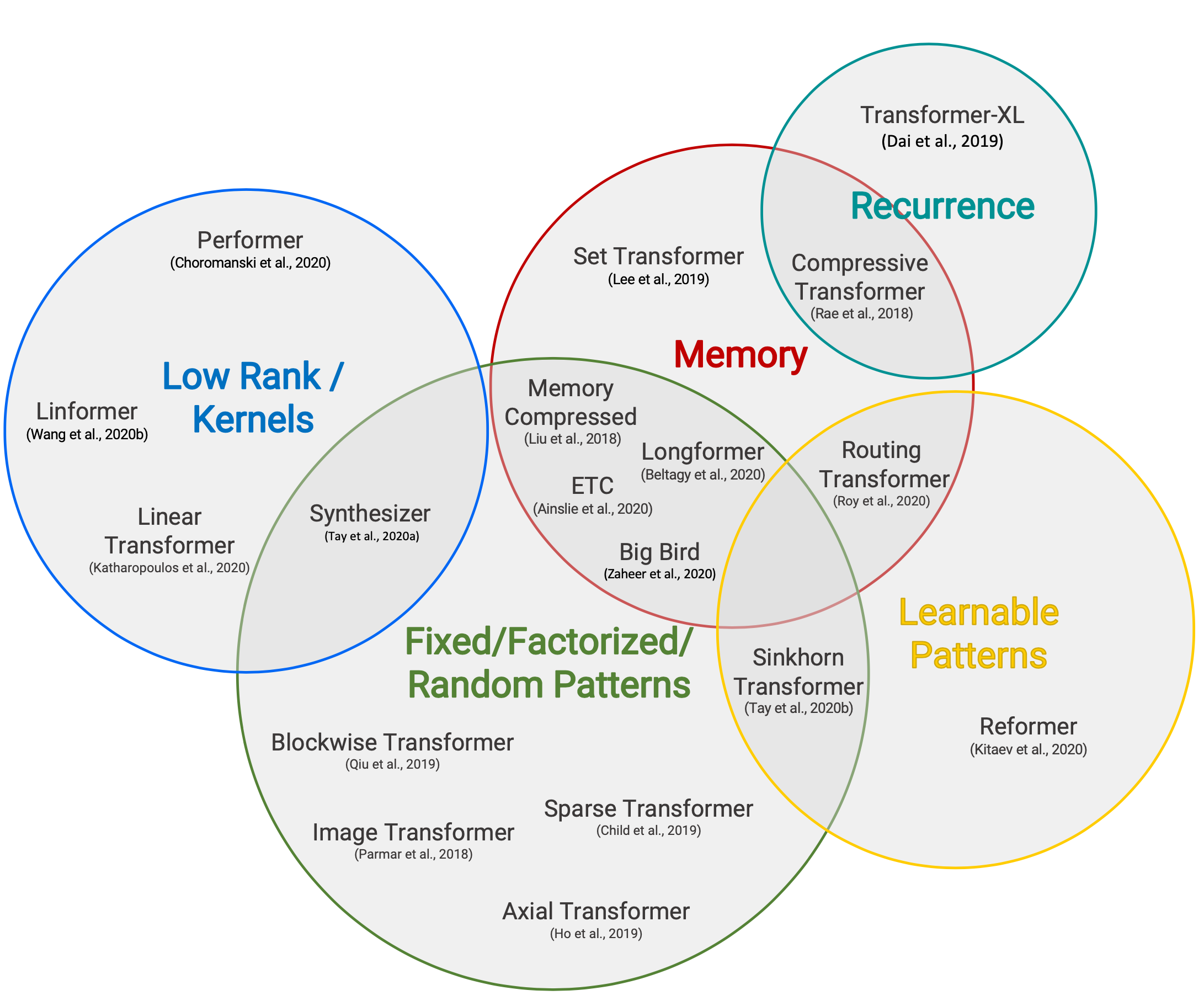
这篇综述论文 高效 Transformers（Tay et al. 2020 ）回顾了一系列新的 transformer 架构，它们为了更好的 计算和内存效率 而进行了改进。强烈推荐阅读。您也可以查看我的文章“Transformer Family Version 2.0” ，以深入了解包括降低模型运行成本的 transformer 架构的多方面改进。

图 18. 高效 transformer 模型的分类。
(图片来源：Tay et al. 2020 )

由于自注意机制具有二次时间和内存复杂度，这是提高 transformer 解码效率的主要瓶颈，所有的高效 transformer 模型都在原本密集的注意层上应用了某种稀疏形式。这里只列举了一个高层次的概述，一些内容源自 Tay et al. 2020 。

稀疏注意模式

1. 固定模式 限制了注意矩阵的视野，使用预定义的固定模式。

   • 将输入序列划分为固定的块，例如 Blockwise Attention ；
   • Image Transformer 使用局部注意；
   • Sparse Transformer 使用跨步注意模式。

2. 组合模式 学习对输入标记进行排序 / 聚类 - 在保持固定模式的效率优势的同时，实现了对序列的更优全局视图。

   • Sparse Transformer 结合了跨步和局部注意；
   • 对于一个高维输入张量，Axial Transformer 不是对输入的扁平化版本应用注意力，而是沿着输入张量的单个轴应用多个注意力；
   • ETC，Longformer 和 Big Bird 结合了局部和全局上下文，以及跨步或随机注意。

3. 可学习模式 通过学习确定最优的注意模式。

   • Reformer 根据基于哈希的相似性（LSH）将标记聚集在一起；
   • Routing Transformer 对标记执行 $k$-均值聚类；
   • Sinkhorn Sorting Network 学习对输入序列的块进行排序。

循环机制

循环机制通过循环连接多个块 / 段。

• Transformer-XL 通过在段之间重用隐藏状态来利用更长的上下文。
• 通用 Transformer 将自我注意力与 RNN 中的循环机制相结合。
• 压缩 Transformer 是 Transformer-XL 的扩展，具有额外的内存，包含一组用于过去激活的内存插槽和用于压缩激活的压缩内存插槽。每当模型接受新的输入段时，主内存中最旧的激活将移至压缩内存，其中应用了压缩函数。

节省内存设计

节省内存设计指的是为了减少内存使用而对架构进行的修改。

• Linformer 将 keys 和 values 的长度维度投影到低维表示 ($N \to k$)，从而将内存复杂度从 $N \times N$ 降低到 $N \times k$。
• Shazeer (2019) 提出了 多查询注意力，该注意力在不同的注意力 “头” 之间共享 keys 和 values，大大减少了这些张量的大小和内存成本。
• 随机特征注意力和 Performer 使用 核方法 以实现自注意机制的更便宜的数学格式。

自适应注意力

自适应注意力 使模型能够学习最佳的注意力跨度，或者决定何时对不同的输入令牌进行提前退出。

• 自适应注意力跨度 通过在令牌和其他 keys 之间的软掩码，训练模型学习每个令牌每个头的最佳注意力跨度。
• 通用 Transformer 结合了循环机制，并使用 ACT（自适应计算时间） 来动态决定循环步骤的数量。
• 深度自适应 Transformer 和 CALM 学习何时使用一些信心度量来为每个令牌提前退出计算层，以实现良好的性能 - 效率权衡。

Citation

Cited as:

Weng, Lilian. (Jan 2023). Large Transformer Model Inference Optimization. Lil’Log. https://lilianweng.github.io/posts/2023-01-10-inference-optimization/ .

Or

1
2
3
4
5
6
7
8

@article{weng2023inference,
  title   = "Large Transformer Model Inference Optimization",
  author  = "Weng, Lilian",
  journal = "Lil'Log",
  year    = "2023",
  month   = "Jan",
  url     = "https://lilianweng.github.io/posts/2023-01-10-inference-optimization/"
}

References

[1] Bondarenko et al. “Understanding and overcoming the challenges of efficient transformer quantization” ACL 2021.

[2] Dettmers et al. “LLM.int8(): 8-bit Matrix Multiplication for Transformers at Scale” NeuriPS 2022

[3] Zadeh et al. “Gobo: Quantizing attention-based NLP models for low latency and energy efficient inference." MICRO 2020

[4] Shen, Dong & Ye, et al. “Q-BERT: Hessian based ultra low precision quantization of BERT” AAAI 2020.

[5] Yao et al. “ZeroQuant: Efficient and affordable post-training quantization for large-scale transformers” arXiv preprint arXiv:2206.01861 (2022).

[6] Frantar et al. “GPTQ: Accurate Quantization for Generative Pre-trained Transformers” arXiv preprint arXiv:2210.17323 (2022).

[7] Xiao & Lin “SmoothQuant: Accelerated sparse neural training: A provable and efficient method to find N:M transposable masks." arXiv preprint arXiv:2211.10438 (2022). | code

[8] Pool & Yu. “Channel Permutations for N:M Sparsity." NeuriPS 2021. | code

[9] Zhou & Ma, et al. “Learning N:M fine-grained structured sparse neural networks from scratch." arXiv preprint arXiv:2102.04010 (2021).

[10] Jayakumar et al. “Top-KAST: Top-K Always Sparse Training." NeuriPS 2020.

[11] Nvidia. “Nvidia A100 tensor core GPU architecture." 2020.

[12] Gale, Elsen & Hooker “The State of Sparsity in Deep Neural Networks." arXiv preprint arXiv:1902.09574 (2019).

[13] Zhu & Gupta. “To Prune, or Not to Prune: Exploring the Efficacy of Pruning for Model Compression." arXiv preprint arXiv:1710.01878 (2017).

[14] Renda et al. “Comparing rewinding and fine-tuning in neural network pruning." arXiv preprint arXiv:2003.02389 (2020).

[15] Zhou & Ma, et al. “Learning N:M fine-grained structured sparse neural networks from scratch." arXiv preprint arXiv:2102.04010 (2021).

[16] Pool & Yu. “Channel Permutations for N:M Sparsity." NeuriPS 2021. | code

[17] Jaszczur et al. “Sparse is Enough in Scaling Transformers." NeuriPS 2021.

[18] Mishra et al. “An Survey of Neural Network Compression." arXiv preprint arXiv:1710.09282 (2017).

[19] Fedus et al. “A Review of Sparse Expert Models in Deep Learning." arXiv preprint arXiv:2209.01667 (2022)..

[20] Riquelme et al. “Scaling vision with sparse mixture of experts." NeuriPS 2021.

[21] Kudugunta et al. “Beyond Distillation: Task-level Mixture-of-Experts for Efficient Inference." arXiv preprint arXiv:2110.03742 (2021).

[22] Rajbhandari et al. “DeepSpeed-MoE: Advancing mixture-of-experts inference and training to power next-generation ai scale." arXiv preprint arXiv:2201.05596 (2022).

[23] Kossmann et al. “Optimizing mixture of experts using dynamic recompilations." arXiv preprint arXiv:2205.01848 (2022).

[24] Hwang et al. “Tutel: Adaptive mixture-of-experts at scale." arXiv preprint arXiv:2206.03382 (2022). | code

[25] Noam Shazeer. “Fast Transformer Decoding: One Write-Head is All You Need." arXiv preprint arXiv:1911.02150 (2019).

[26] Tay et al. “Efficient Transformers: A Survey." ACM Computing Surveys 55.6 (2022): 1-28.

[27] Pope et al. “Efficiently Scaling Transformer Inference." arXiv preprint arXiv:2211.05102 (2022).

[28] Frankle & Carbin. “The Lottery Ticket Hypothesis: Finding Sparse, Trainable Neural Networks” ICLR 2019.

[29] Elabyad et al. “Depth-Adaptive Transformer” ICLR 2020.

[30] Schuster et al. “Confident Adaptive Language Modeling” arXiv preprint arXiv:2207.07061 (2022).

[31] Gou et al. “https://arxiv.org/abs/2006.05525” arXiv preprint arXiv:2006.05525 (2020).

[32] Hinton et al. “Distilling the Knowledge in a Neural Network” NIPS 2014.

[33] Sanh et al. “DistilBERT, a distilled version of BERT: smaller, faster, cheaper and lighter” Workshop on Energy Efficient Machine Learning and Cognitive Computing @ NeuriPS 2019.

• language-model
• long-read
• architecture
• attention
• transformer
• foundation